Eternity

Until The End

OIP2022.03.05模拟赛

发表于 更新于 分类于
本文字数： 13k 阅读时长 ≈ 12 分钟

“提高模拟能考出省选题来“

题目I——最短路径(path)

题目描述

一个 $N$ 个点，$M$ 条边的有向权值图，求全源最短路中每条边被经过的次数。

最短路径：从 $a$ 到 $b$ 的最短路径是指一条路径当且仅当不存在另一条从 $a -> b$ 的路径比该路径更短。

意思是两点之间的最短路径不止一条

求每条边通过的最短路径的个数。取模 $10^9+7$。

思路I

用 $Spfa$ 跑 $n$ 遍最短路，跑完之后枚举每条边，记录所有满足 $val_i+c_{i,j}=val_j$ 的边。再以此对于每一遍 $Spfa$ 跑一遍 $Topo$ 排序。

思路II

依然是跑 $n$ 遍最短路，求出最短路径图，即只含最短路的边。用 $f_i$ 表示从 $1$ 点至 $i$ 点有多少条路径， $g_i$ 表示从 $i$ 号点往后走有多少条路径。则以 $i$ 为起点的所有最短路中，经过 $c_j(u,v)$ 边的路径条数为 $f_u*g_v$

另话

这道题在洛谷上是双倍经验。一道紫一道灰。这样做 $NOIp$ 模拟的第一题真的好吗

Task One Ac Code

思路I 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define underMax(x,y) ((x)>(y)?(x):(y))
#define underMin(x,y) ((x)<(y)?(x):(y))
typedef long long ll;
using namespace std;
const int MAXN=1501,MAXM=5001;
const int Mod=1e9+7;
template<class T>
inline void underRead(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=gh();
    if(t) x=-x;
}
int N,M,u,v,w;
struct Node
{
    int from,to,next,val;
}Edge[MAXM<<1];
int First[MAXN],Total,Dist[MAXN],Que[MAXM<<1];
bool Vis[MAXN],Is[MAXM];
inline void underAdd(int x,int y,int z)
{
    Edge[++Total]=(Node){x,y,First[x],z};First[x]=Total;
}
inline void underSPFA(int x)
{
    memset(Dist,0x7f7f7f7f,sizeof(Dist));
    memset(Is,0,sizeof(Is));
    register int len;
    Dist[Que[len=1]=x]=0,Vis[x]=1;
    for(int i=1;i<=len;++i)
	{
	    int u=Que[i];Vis[u]=0;
	    for(int e=First[u],v;e;e=Edge[e].next)
		{
		    if(Dist[u]+Edge[e].val<Dist[v=Edge[e].to])
			{
			    Dist[v]=Dist[u]+Edge[e].val;
			    if(!Vis[v]) Vis[Que[++len]=v]=1;
			}
		}
	}
    for(int i=1;i<=M;++i)
	{
	    if(Dist[Edge[i].from]+Edge[i].val==Dist[Edge[i].to])
		{
		    Is[i]=1;
		}
	}
}
int Deg[MAXN],Cnt[3][MAXN],Ord[MAXN],len,Ans[MAXM];
queue<int>Q;
inline void underTopo(int s)
{
    while(!Q.empty()) Q.pop();
    memset(Deg,0,sizeof(Deg));
    memset(Cnt,0,sizeof(Cnt));
    len=0;
    for(int i=1;i<=M;++i) if(Is[i]) ++Deg[Edge[i].to];
    Q.push(s); Cnt[1][s]=1;
    while(!Q.empty())
	{
	    int u=Q.front();Q.pop();
	    Ord[++len]=u;
	    for(int e=First[u];e;e=Edge[e].next)
		{
		    if(!Is[e]) continue;
		    int v=Edge[e].to;
		    Cnt[1][v]=(Cnt[1][v]+Cnt[1][u])%Mod;
		    if(--Deg[v]==0) Q.push(v);
		}
	}
    for(int j=len;j>=1;--j)
	{
	    int x=Ord[j];++Cnt[2][x];
	    for(int e=First[x];e;e=Edge[e].next)
		{
		    if(!Is[e]) continue;
		    Cnt[2][x]=(Cnt[2][x]+Cnt[2][Edge[e].to])%Mod;
		}
	}
}
int main()
{
	freopen("path.in","r",stdin);
	freopen("path.out","w",stdout);
    scanf("%d%d",&N,&M);
    for(int i=1;i<=M;++i)
	{
	    scanf("%d%d%d",&u,&v,&w);
	    underAdd(u,v,w);
	}
    for(int i=1;i<=N;++i)
	{
	    underSPFA(i);underTopo(i);
	    for(int j=1;j<=M;++j)
		{
		    if(Is[j]) Ans[j]=(Ans[j]+1ll*Cnt[1][Edge[j].from]*Cnt[2][Edge[j].to]%Mod)%Mod;
		}
	}
    for(int i=1;i<=M;++i) printf("%d\n",Ans[i]);
    return 0;
}
/*
4 4
1 2 5
2 3 5
3 4 5
1 4 8
*/

思路II 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>

using namespace std;
const int P = 1000000007;

struct Edge {
    int x, y, w, next, ans;
    bool flag;
} map[5101];

int n, m, st, ed;
int d[1510], r[1510], dis[1510], f[1510], g[1510], head[1510];
bool flag[1510];

bool cmp(int a, int b) {
    return dis[a] < dis[b];
}

void add_edge(int x, int y, int w, int c) {
    map[c].x = x;
    map[c].y = y;
    map[c].w = w;
    map[c].ans = 0;
    map[c].next = head[x];
    head[x] = c;
}

int main() {
	freopen("path.in", "r", stdin);
	freopen("path.out", "w", stdout);
    scanf("%d%d", &n, &m);
    for (int i=0; i<n; i++)
        head[i] = -1;
    for (int i=0; i<m; i++) {
        int x, y, w;
        scanf("%d%d%d", &x, &y, &w);
        x --; y --;
        add_edge(x, y, w, i);
    }
    for (int i=0; i<n; i++) r[i] = i;
    for (int start=0; start<n; start++) {
        for (int i=0; i<n; i++) dis[i] = 99999999;
        dis[start] = 0;
        for (int i=0; i<n; i++) flag[i] = true;
        flag[start] = false;
        st = ed = 0;
        d[ed++] = start;
        while (st < ed) {
            int i = d[(st++) % n];
            for (int j=head[i]; j>-1; j=map[j].next)
                if (dis[i] + map[j].w < dis[map[j].y]) {
                    dis[map[j].y] = dis[i] + map[j].w;
                    if (flag[map[j].y]) {
                        flag[map[j].y] = false;
                        d[(ed++) % n] = map[j].y;
                    }
                }
            flag[i] = true;
        }
        //for (int i=0; i<n; i++)
        //    printf("%d-->%d: %d\n", start, i, dis[i]);
        //printf("start: %d\n", start);
        for (int i=0; i<m; i++)
            if (dis[map[i].x] + map[i].w == dis[map[i].y]) {
                map[i].flag = true;
        //        printf("%d-->%d(%d)  ", map[i].x, map[i].y, map[i].w);
            }
            else
                map[i].flag = false;
        //printf("\n");
        sort(r, r+n, cmp);
        
        for (int i=0; i<n; i++) f[i] = 0;
        f[start] = 1;
        for (int i=0; i<n; i++) {
            for (int j=head[r[i]]; j>-1; j=map[j].next)
                if (map[j].flag)
                    f[map[j].y] = (f[map[j].y] + f[r[i]]) % P;
        }
        //for (int i=0; i<n; i++)
        //    printf("f[%d]=%d  ", i, f[i]);
        //printf("\n");
        
        for (int i=n-1; i>0; i--) {
            g[r[i]] = 1;
            for (int j=head[r[i]]; j>-1; j=map[j].next)
                if (map[j].flag)
                    g[r[i]] = (g[r[i]] + g[map[j].y]) % P;
        }
        //for (int i=0; i<n; i++)
        //    printf("g[%d]=%d  ", i, g[i]);
        //printf("\n");
        
        for (int i=0; i<m; i++)
            if (map[i].flag) {
                //printf("%d-->%d  ", map[i].x, map[i].y);
                map[i].ans = (map[i].ans + g[map[i].y] * (long long)(f[map[i].x])) % P;
            }
        //printf("\n");
    }
    for (int i=0; i<m; i++)
        printf("%d\n", map[i].ans);
}

题目II——数列(seq)

题目描述

对于一个长度为 $n$ 的数列，有 $m$ 个询问：

  1. $C\ i\ x$ 表示将下标为 $i$ 的数改为 $x$
  2. $Q\ i$ 求满足 $\forall i \leq k \leq j,A_k \leq \max\{A_i,A_j\}$ 中 $j$ 的个数

复杂度不大于 $O(n \log n)$

题意思路

根据其查询，我们需要找到所有的“谷段”，即如果我们将整个数列看作一个波峰图，如下图所示：

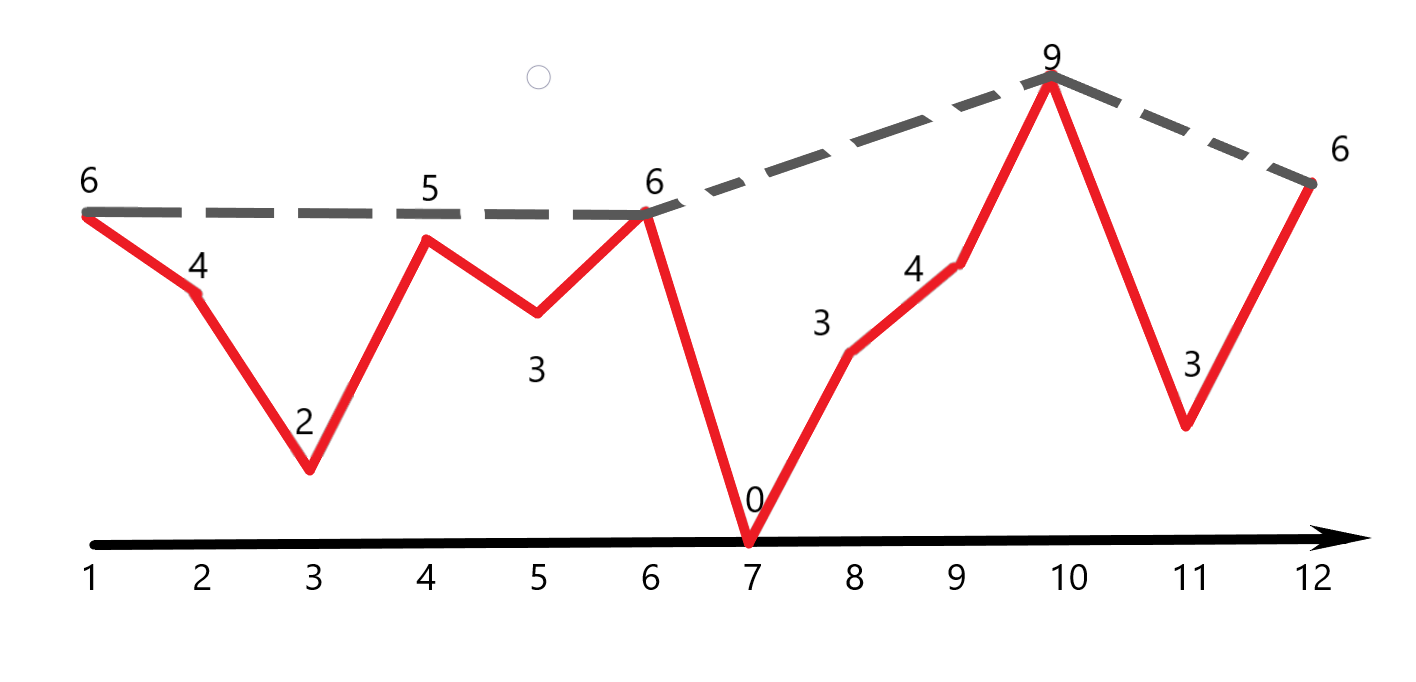
那么我们就需要找到所有类似于开口向上的二次函数的个数。不难发现：当我们第一次找到 $A_p \leq A_j$ 时，$p$ 到 $j$ 之间的任意位置都是满足要求的。

然而，当第一次：

当 $A_p = A_j$ 时，对于 $j$ 之后下一个满足要求的位置 $k$ 时，$j$ 与 $k$ 之间的任意位置也是可以取的。

而当 $A_p < A_j$ 时，对于 $j$ 之后下一个满足要求的位置 $k$ 时，就仅仅只能取 $k$ 位置了。

其缘由读者可自行思考。

算法思路

又是线段树打爆的一天

使用一种类似分块但胜似分块的神奇思路。

将整个数列分成 $\sqrt n$ 段：

  1. 对于每一段，维护其向左向右的递增序列；
  2. 对于相邻的段，维护其向左向右的递增序列。

虽然我觉得这题解类似没写又胜似没写

用 $L_i$ 存储第 $i$ 段的左坐标，$R_i$ 存储第 $i$ 段的右坐标。数组 $Bel_i$ 存储 $i$ 位置所属的段编号。

初始化/修改操作

对于每一段都有一个数 $top$ 和一个数组 $st_i$ 。$st$ 数组存储的是该区间内的最长不下降子序列，而 $top$ 则是 $st$ 数组的长度。然后求就完事儿了，复杂度 $O(\sqrt n)$

1
2
3
4
5
6
7
8
9
inline void underModify(int l,int r,int st[],int &top)
{
	top=0;
	for(int i=r;i>=l;--i)
	{
		while(top&&Num[st[top]]<Num[i]) --top;
		st[++top]=i;
	}
}

查询操作

暴力求本区间，复杂度 $O(\sqrt n )$

1
2
3
4
5
6
7
int ans=0;
int bl=Bel[p],Max=Num[p];
for(int i=p+1;i<=R[bl];++i)
{
    Max=underMax(Max,Num[i]);
    if(Max<=underMax(Num[p],Num[i])) ++ans;
}

记查询点为 $p$ ,则对于 $Bel_p+1$ 到 $Bel_n$ 的区间操作为：

二分该区间的 $st$ 数组，找到第一个 $l$ 位置满足 $A_p \leq A_l$ ，如果当前 $Max$ 与 $A_p$ 是相等的，则可以计算该区间 $l$ 之前的任意位置；反之，计算 $l$ 之后的个数和（不比 $A_p$ 小的个数），当然，$Max=A_p$ 时也要计算该区间。

然后更改 $Max$ 值，查找下一区间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
for(int i=bl+1;i<=num;++i)
{
    int l=0,r=Top[i];
    if(Max==Num[p])
    {
        while(l<r)
        {
            int mid=(l+r+1)>>1;
            if(Num[St[i][mid]]>Max) l=mid;
            else r=mid-1;
        }
        if(l==0) ans+=R[i]-L[i]+1;
        else
        {
            ans+=St[i][l]-1-L[i]+1;
            ans+=l-1+1;
        }
    }
    else
    {
        while(l<r)
        {
            int mid=(l+r+1)>>1;
            if(Num[St[i][mid]]>=Max) l=mid;
            else r=mid-1;
        }
        ans+=l-1+1;
    }
    Max=underMax(Max,Num[St[i][1]]);
}
return ans;

另话

这道题题意很简单，主要原因还是时间复杂度的问题。我使用线段树二分查找的复杂度不稳定，所以很氢凇被卡了

Task Two Ac Code

查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
typedef long long ll;
using namespace std;
const int MAXN=50001;
const int MAXM=101;
const int MAXB=1001;
const int INF=0x7f7f7f7f;
template<class T>
inline void underRead(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
int N,M,Num[MAXN],Qi,Qx;
char op;
int Bel[MAXN],L[MAXM],R[MAXM],St[MAXM][MAXB],Top[MAXM];
/*struct SegmentTree
{
	int l,r,dat;
}Tree[MAXN<<2];*/
inline int underMax(int a,int b)
{
	return (a>b?a:b);
}
inline int underMin(int a,int b)
{
	return (a<b?a:b);
}
/*inline void underPushUp(int p)
{
	Tree[p].dat=underMax(Tree[p<<1].dat,Tree[p<<1|1].dat);
}
inline bool underCheck(int p)
{
	if(Tree[p].dat==Num[Tree[p].l]||Tree[p].dat==Num[Tree[p].r]) return 1;
	return 0;
}
inline void underBuild(int p,int l,int r)
{
	Tree[p].l=l,Tree[p].r=r;
	if(l==r)
	{
		Tree[p].dat=Num[l];
		return ;
	}
	int mid=(l+r)>>1;
	underBuild(p<<1,l,mid),underBuild(p<<1|1,mid+1,r);
	underPushUp(p);
}
inline void underModify(int p,int d,int x)
{
	if(Tree[p].l==d&&Tree[p].r==d)
	{
		Tree[p].dat=x;
		return ;
	}
	int mid=(Tree[p].l+Tree[p].r)>>1;
	if(d<=mid) underModify(p<<1,d,x);
	if(mid<d) underModify(p<<1|1,d,x);
	underPushUp(p);
}
inline int underQueryMax(int p,int l,int r)
{
	if(l<=Tree[p].l&&Tree[p].r<=r) return Tree[p].dat;
	int mid=(Tree[p].l+Tree[p].r)>>1;
	int val=-INF;
	if(l<=mid) val=underMax(val,underQueryMax(p<<1,l,r));
	if(mid<r) val=underMax(val,underQueryMax(p<<1|1,l,r));
	return val;
}
inline void underNeverGonnaGiveYouUp()
{
	for(int i=1;i<=M;++i)
	{
		scanf("%c",&op);
		if(op=='Q')
		{
			underRead(Qi);
			int Ans=0,Maxn=Num[Qi];
			for(int j=Qi+1;j<=N;++j)
			{
				Maxn=underMax(Maxn,Num[j]);
				if(Maxn<=Num[Qi]||Maxn<=Num[j]) ++Ans;
			}
			printf("%d\n",Ans);
		}
		else
		{
			underRead(Qi),underRead(Qx);
			Num[Qi]=Qx;
		}
	}
	exit(0);
}
inline int underExpr(int p,int x)
{
	if(x==N) return 0;
	if(underQueryMax(1,x+1,N)<Num[x])
	{
		if(p>1) return 0;
		else return N-x;
	}
	int l=x+1,r=N;
	while(l<r)
	{
		int mid=(l+r)>>1;
		int val=underQueryMax(1,x+1,mid);
		if(val<Num[x]) l=mid+1;
		else r=mid;
	}
//	printf("[%d,%d] ",x,l);
	if(p>1) return 1+underExpr(p,l);
	else if(Num[l]==Num[x]) return l-x+underExpr(p,l);
	else return l-x+underExpr(p+1,l);
}*/
inline void underModify(int l,int r,int st[],int &top)
{
	top=0;
	for(int i=r;i>=l;--i)
	{
		while(top&&Num[st[top]]<Num[i]) --top;
		st[++top]=i;
	}
}
inline int underQuery(int p,int num)
{
	int ans=0;
	int bl=Bel[p],Max=Num[p];
	for(int i=p+1;i<=R[bl];++i)
	{
		Max=underMax(Max,Num[i]);
		if(Max<=underMax(Num[p],Num[i])) ++ans;
	}
	for(int i=bl+1;i<=num;++i)
	{
		int l=0,r=Top[i];
		if(Max==Num[p])
		{
			while(l<r)
			{
				int mid=(l+r+1)>>1;
				if(Num[St[i][mid]]>Max) l=mid;
				else r=mid-1;
			}
			if(l==0) ans+=R[i]-L[i]+1;
			else
			{
				ans+=St[i][l]-1-L[i]+1;
				ans+=l-1+1;
			}
		}
		else
		{
			while(l<r)
			{
				int mid=(l+r+1)>>1;
				if(Num[St[i][mid]]>=Max) l=mid;
				else r=mid-1;
			}
			ans+=l-1+1;
		}
		Max=underMax(Max,Num[St[i][1]]);
	}
	return ans;
}
int main()
{
	freopen("seq.in","r",stdin);
	freopen("seq.out","w",stdout);
    scanf("%d%d",&N,&M);
	int siz=sqrt(N*log2(N)),num=(N+siz-1)/siz;
    for(int i=1;i<=N;++i) scanf("%d",&Num[i]),Bel[i]=(i+siz-1)/siz;
	for(int i=1;i<=num;++i)
	{
		L[i]=R[i-1]+1,R[i]=underMin(i*siz,N);
		underModify(L[i],R[i],St[i],Top[i]);
	}
//	if(N<=5000) underNeverGonnaGiveYouUp();
    /*underBuild(1,1,N);*/
	for(int T=1;T<=M;++T)
	{
		cin>>op;
		if(op=='Q')
		{
			scanf("%d",&Qi);
			/*if(underQueryMax(1,Qi,N)==Num[Qi]) printf("%d\n",N-Qi);
			else if(Tree[1].dat==Num[Qi])printf("%d\n",N-Qi);
			else printf("%d\n",underExpr(1,Qi));
			printf("%d\n",underQuery(1,Qi-1,Qi+1));*/
			printf("%d\n",underQuery(Qi,num));
		}
		else
		{
			scanf("%d%d",&Qi,&Qx);
			Num[Qi]=Qx;
			int bl=Bel[Qi];
			underModify(L[bl],R[bl],St[bl],Top[bl]);
		}
	}
    return 0;
}
/*
5 3
1 3 2 3 2
Q 1
C 1 3
Q 1

10 12
1 2 3 4 5 6 7 8 9 10
Q 1
C 1 10
Q 1
C 2 11
Q 1
C 3 11
Q 1
C 4 10
C 5 11
Q 1
C 1 11
Q 1

1 5 3 6 3 3 6
st[1]=6 top=1 i=7
st[2]=6,3 top=2 i=6
st[3]=6,3,3 top=3 i=5
st[2]=6,6 top=2 i=4
st[3]=6,6,3 top=3 i=3
st[3]=6,6,5 top=3 i=2
st[4]=6,6,5,1 top=4 i=1
*/

相关文章