Eternity

Until The End

数论分块&狄利克雷卷积

发表于 更新于 分类于 ，
本文字数： 6.2k 阅读时长 ≈ 6 分钟

万事俱备，则时空将会反演。

数论分块

字面意思，在数学论理中进行分块处理。一般用于快速计算含有向下取整和式的题。当可以在 $\mathcal O(1)$ 内计算出 $f(r)-f(l)$ 或者已经预处理除了 $f$ 的前缀和时，数论分块就能够使用 $\mathcal O(\sqrt n)$ 的时间内计算出类似于 $\sum\limits^{n}_{i=1}f(i)g(\lfloor \frac{n}{i} \rfloor)$ 的和式的值。

富比尼定理(Fubini’s theorem)

将 $\lfloor\frac{n}{i}\rfloor$ 打包计算。

又称“算两次”，以意大利数学家圭多·富比尼（$\text{Guido Fubini}$）命名。 富比尼定理的积分形式：只要二重积分 $ \int\int|f(x,y)|dxdy$ 有界，则可以逐次计算二重积分，并且可以交换逐次积分的顺序。 积分号也是特殊的求和号，因此在一般求和中，富比尼定理往往呈现为更换计数顺序，即交换两个求和号。 组合数学中的富比尼定理表现为，用两种不同的方法计算同一个量，从而建立相等关系。这种方法在反比例函数上有很好的解释：

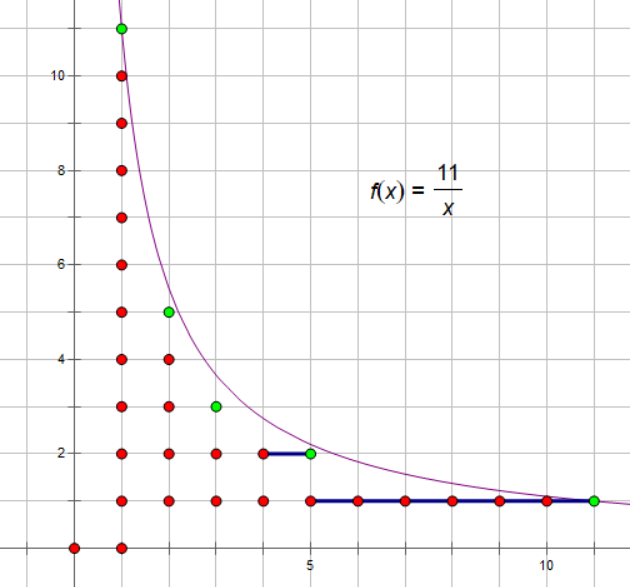
在区间 $[1,11]$ 中，根据 $y=\lfloor\frac{11}{x}\rfloor$ 的答案不同，被分成了 $5$ 块， $5$ 块整点的最大纵坐标都相同，

引理 Ⅰ

$\forall a,b,c\in\mathbb Z,\lfloor\frac{a}{bc}\rfloor=\lfloor\frac{\lfloor\frac{a}{b}\rfloor}{c}\rfloor$ ，证明详见 OI-Wiki

引理 Ⅱ

$\forall n\in \mathbb N_+,|\{\lfloor\frac{n}{d}\rfloor|d\in\mathbb N_+,d\leq n\}|\leq\lfloor2\sqrt n\rfloor$ ，证明详见 OI-Wiki

引理 Ⅲ

对于 $\forall i\le n,\lfloor\frac{n}{i}\rfloor$ 只存在 $\mathcal O(\sqrt n)$ 种不同的值。

对于 $i\le \sqrt n$ 的部分，$i$ 只存在 $\sqrt n$ 个，取值也不会超过 $\sqrt n$ 个；

对于 $i>\sqrt n$ 的部分，$\lfloor\frac{n}{i}\rfloor<\sqrt n$ ，取值也不会超过 $\sqrt n$ 个。

结论

对于常数 $n$ ，使 $\lfloor\frac{n}{i}\rfloor=\lfloor\frac{n}{j}\rfloor$ 成立的最大满足 $i\leq j\leq n$ 的 $j$ 的值为 $\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor$ 。即值 $\lfloor\frac{n}{i}\rfloor$ 所在块的右端点为 $\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor$ 。

简单证明：

因为有 $\lfloor\frac{n}r\rfloor=\lfloor\frac{n}{i}\rfloor$ ，则有：

$r\times\lfloor\frac{n}{i}\rfloor\le n$ ，变式得到：

$r\le\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor$ 。

证毕。

分块加速

那么，就如同对数组进行分块一样，对于每一个块的计算，我们就直接用块值乘以个数计算即可，用数论分块加速时间，降低时间复杂度。

例题

UVA11526

题意显而易见了。直接分块计算即可。记得开 long long 。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
#define db double
typedef long long ll;
using namespace std;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
int T,n;
inline ll H(int n)
{
    ll res=0;
    ll l=1,r;
    while(l<=n)
    {
        r=n/(n/l);
        res+=1ll*(r-l+1)*(n/l);
        l=r+1;
    }
    return res;
}
int main()
{
    // freopen("sqrt-decomposition.in","r",stdin);
    // freopen("sqrt-decomposition.out","w",stdout);
    read(T);
    while(T--)
    {
        read(n);
        printf("%lld\n",H(n));
    }
    return 0;
}
/*
2
5
10
*/

Luogu 2261

这道题需要一点特判。

我们知道 $k\bmod p =k-\lfloor\frac{k}{p}\rfloor\times p$ ，那么，我们需要求的式子也可以转化为：

$ans=\sum_{i=1}^n k\bmod i=\sum_{i=1}^n k-\lfloor\frac{k}{i}\rfloor\times i=nk-\sum_{i=1}^n \lfloor\frac{n}{i}\rfloor\times i$

然后就转化为了数论分块的经典各式了。

对于这道题的特判，因为 $n$ 和 $k $ 的大小关系是不清楚的，而因为 $l\leq n$ 可能会存在 $\lfloor\frac{k}{l}\rfloor$ 为 $0$ 的情况，所以需要特判。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
#define db double
typedef long long ll;
using namespace std;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
ll N,K,res,ans;
int main()
{
    // freopen("math.in","r",stdin);
    // freopen("math.out","w",stdout);
    read(N,K);
    ll l=1,r;
    while(l<=N)
    {
        if(K/l) r=min(N,K/(K/l));
        else r=N;
        res+=1ll*(l+r)*(r-l+1)*(K/l)/2;
        // printf("[%d,%d]=%d\n",l,r,res);
        l=r+1;
    }
    ans=N*K-res;
    printf("%lld",ans);
    return 0;
}
/*
k/2+1...k
0...(k+1)/2-1
l...r
*/

N 维数论分块

不太能了解，也不大可能会考（刀我），如果感兴趣的可以自行去 OI Wiki 上浏览。

数论函数

数论函数是指定义域为正整数的函数。

积性函数

积性函数是一种特殊的数论函数，满足 $f(x,y)=f(x)\times f(y),x\perp y$ ，则 $f$ 是积性函数。显然满足 $f(1)=1$ 。

对于 $x\perp y$ 的理解 其实可以把它看作是 $x$ 的向量与 $y$ 的向量相垂直之类的（？感谢李姐。


若 $f(x),g(x)$ 为积性函数，则：

$h(x)=f(x^p)$

$h(x)=f^p(x)$

$h(x)=f(x)g(x)$

$\displaystyle h(x)=\sum_{d\mid x}f(d)g(\frac{x}{d})$

中的 $h(x)$ 都是积性函数。

对于任意正整数 $x,y$ 满足 $f(xy)=f(x)\times f(y)$ ，则 $f$ 为完全积性函数。

常见常用的积性函数：

  1. 单位函数 $\epsilon(n)=[n=1]$ ，即当 $n=1$ 时 $\epsilon(n)=1$ ，否则 $\epsilon(n)=0$ 。
  2. 恒等函数 $id_k(n)=n^k,id_1(n)$ 通常简记作 $id(n)$ 。
  3. 常数函数 $I(n)=1$ 。
  4. 除数函数 $\sigma_k(n)=\sum_{d\mid n}d^k,\sigma_0(n)$ 通常简记作 $d(n)$ ，而 $\sigma_1(n)$ 通常简记作 $\sigma(n)$ 。
  5. 欧拉函数 $\varphi(n)=\sum_{i\le n}[\gcd(i,n)=1]$ ，常用的一个计算式是 $\varphi(n)=n\times \prod_{p\in \operatorname{Prime}}\frac{p-1}{p}$ 。
  6. 莫比乌斯函数 $\mu(n)$ ，当 $n=1$ 时，$\mu(1)=1$ ，当 $n>1$ 时，记 $n$ 的质因子分解为 $n=\prod p_i^{k_i}$ ，共有 $\omega(n)$ 种质因子，则当存在 $k_i>1$ 时，$\mu(n)=0$ ，否则 $\mu(n)=(-1)^{\omega(n)}$ 。

狄利克雷函数

狄利克雷生成函数

一个数列的狄利克雷生成函数（被称为 $DGF$ ） 被定义为：

$f_i$ 是一个从 $\mathbb N_+$ 到 $\mathbb Z$ 的函数，该生成函数与一个数论函数相对应，规定 $f_1=1$ 。

如果该函数是积性函数，（积性函数定义：对于所有互质的整数 $a$ 和 $b$ 有性质 $f(ab)=f(a)f(b)$ 的数论函数）即满足 $\forall i\perp j,f(ij)=f(i)\times f(j)$ ，则 $\tilde{F}(x)$ 可以由质数及其幂来表达，记作：（令 $P$ 为全体质数集合）

狄利克雷卷积

若数论函数 $f,g,h$ 满足 $h(n)=\sum_{d\mid n}f(d)g(\frac{n}{d})$ ，则称 $h$ 为 $f,g$ 的狄利克雷卷积。记作 $h=f\ast g$ 。

满足性质：

  1. 单位函数 $\epsilon$ 是狄利克雷卷积的单位元（幺元），即 $f\ast\epsilon=f$ 。
  2. 狄利克雷卷积满足结合律和交换律。即 $a\ast b=b\ast a,a\ast(b\ast c)=(a\ast b)\ast c$ 。
  3. 两个积性函数的狄利克雷卷积仍是积性函数。

性质三的证明类似于除数函数的积性证明。

逆元 · 重定义

在狄利克雷卷积的条件下，我们对逆元进行重定义：

满足 $f\ast f^{-1}= \epsilon$ ，则称 $f_{-1}$ 为 $f$ 的逆元。

如果 $f$ 是积性函数，则其逆元 $f^{-1}$ 也是积性函数。

相关文章