Eternity

Until The End

李超线段树

发表于 分类于 ，
本文字数： 8.5k 阅读时长 ≈ 8 分钟

经斩错乱的荆棘丛生，拨散诡谲的迷雾栾鸾。

李超线段树

用于求解某一个点在若干函数上的最值，支持动态修改函数的数据结构。

问题

维护如下操作：

  • 加入一个一次函数 $k,b$ ，定义域为 $[l,r]$ ；
  • 查询 $k$ ，求 $x=k$ 时线段的最大值，并输出该一次函数的编号。

$n\leq 10^5,1\leq k,x_0,x_1\leq 39989,1\leq y_0,y_1\leq 10^9$ 。

首先，应该考虑对于一次函数 $(x_1,y_1)\to(x_2,y_2),x_1=x_2$ 的情况，即当前线段垂直与 $x$ 轴，则选择添加一个定义域为 $[x,x]$ 的函数 $f(x)=0\cdot x+\max\{y_1,y_2\}$ 。

分析

有给定值域，支持合并性质。

考虑分块。考虑线段树。

对于询问，类似于单点查找，直接递归求解答案即可。

那么，对于每一个结点，我们维护：

$l,r$ $val$
当前结点表示的区间为 $[l,r]$ 与直线 $x=mid$ 的交点纵坐标最大的线段

这是显然的。

而对于在一个区间内添加一条一次函数，即在当前区间 $[l,r]$ 内的 $f_1(x)=k_1x+b$ 上更新答案 $f_2(x)=k_2x+b$ ，需要进行一部分分类讨论。

通俗的讲，我们需要讨论当前线段与最新线段之间对当前区间，对左子区间，对右子区间分别的影响。

一共分 $5$ 种情况，除了一种是完全覆盖之外，其余就是 $(k_1,k_2),\left(f_1(mid),f_2(mid)\right)$ 的大小关系的四种排列，这些读者都可以自行进行模拟。

标记永久化

对于当前区间 $[l,r]$ 的新建线段，我们需要递归下去更新其子区间，并标记上 $tag$ ，但是，当子区间也已经存在了 $tag$ 了，而此 $tag$ 难以合并，只能够下传。

避免冲突，我们需要递归下传标记。

所谓标记永久化，是一个线段树的优化思想，即保证惰性标记不会因为某些原因溢出（例如加法标记不会爆 long long 之类的），就可以使用标记永久化，而不需要下传标记，只需要在询问的时候把标记的影响加到答案中，类似于差分求原数时输出的是原数和差分数的和。

这样操作可以降低程序常数，不同题目的标记永久化操作都不太一样。而同样，这个优化也适用于树套树和可持久化数据结构。

我们回到传递线段的问题上：

上述已经提到，我们需要对子区间进行分类讨论，如果两条线段在当前区间有交点，那么这两条线段都会在一段子区间内成为答案。可以推出【肯定有一个子区间被左子区间或右子区间完全包含】。可以理解下图思考。

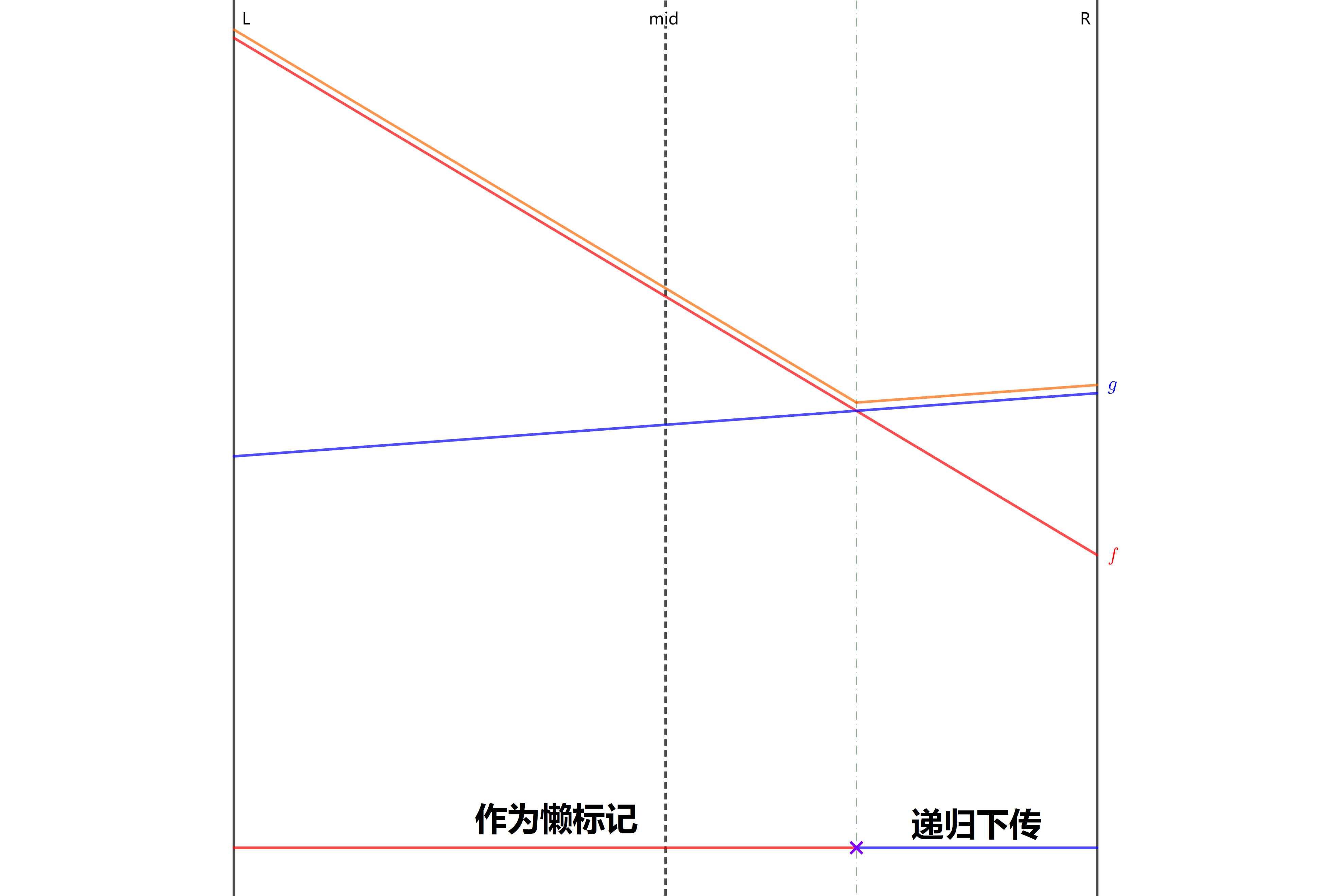
图片来自 $\text{OI-Wiki}$

完全覆盖的区间递归下传，剩余部分作为惰性标记。

这样既保证了惰性标记永久化而不冲突，又使得每一条线段都不被遗漏。

实现

修改

分为下传标记和拆分线段两部分，可以写作两个函数，也可以写作一个。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct Line
{
    int l,r,tag;
    double k,b;
}Tree[MAXN<<2];
inline double calc(Line a,int x);	//求线段a横坐标为x时的纵坐标
inline int cross(Line a,Line b);	//求线段交点
void modify(int p,int l,int r,Line k)
{
    if(k.l<=l&&r<=k.r)
    {
        if(!Tree[p].tag) Tree[p]=k,Tree[p].tag=1;
        else if(calc(k,l)-calc(Tree[p],l)>eps&&calc(k,r)-calc(Tree[p],r)>eps) Tree[p]=k;
        else if(calc(k,l)-calc(Tree[p],l)>eps||calc(k,r)-calc(Tree[p],r)>eps)
        {
            int mid=(l+r)>>1;
            if(calc(k,mid)-calc(Tree[p],mid)>eps) std::swap(k,Tree[p]);
            if(mid-cross(k,Tree[p])>eps) modify(ls,l,mid,k);
            else modify(rs,mid+1,r,k);
        }
    }
    else
    {
        int mid=(l+r)>>1;
        if(k.l<=mid) modify(ls,l,mid,k);
        if(mid<k.r) modify(rs,mid+1,r,k);
    }
}

对于包含区间，就根据上述情况讨论，否则递归下传。

时间复杂度 $\mathcal{O}(\log^2n)$ 。

查询

记住要记录惰性标记的答案贡献。

1
2
3
4
5
6
7
8
9
10
11
double query(int p,int l,int r,int k)
{
    if(l==r) return calc(Tree[p],k);
    else
    {
        int mid=(l+r)>>1;
        double ans=calc(Tree[p],x);
        if(k<=mid) return std::max(ans,query(ls,l,mid,k));
        else return std::max(ans,query(rs,mid+1,r,k));
    }
}

时间复杂度 $\mathcal O(\log n)$ 。

补充

$\text{Lc}$ 线段树的时间复杂度是 $\mathcal O(n\log^2 n)$ 的，但常数极小，甚至能够搭配树链剖分过掉 $\text{1s-10}^5$ ，且李超线段树也能够各种灵活运用，范围也不比线段树少。

例题

Segment

从 $\text{Dyd}$ 从 $\text{l18q}$ 学来的学来的写法。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline void write(T x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
const int MAXN=1e5+10;
const int Mod[3]={0,39989,1000000007};
const double eps=1e-12,INF=1e18;
int lastans;
int N,Cnt;
inline int Cmp(double x,double y)
{
    if(std::fabs(x-y)<eps) return 0;
    return x>y?1:-1;
}
struct Line
{
    double k,b,l,r;
    inline double calc(int x)
    {
        if(x>r||x<l) return -INF;
        return x*k+b;
    }
}Li[MAXN];
struct LcTree
{
    struct Segment
    {
        int l,r,id;
    }Tree[MAXN<<2];
    #define ls p<<1
    #define rs p<<1|1
    void build(int p,int l,int r)
    {
        Tree[p]={l,r,0};
        if(l==r) return ;
        int mid=(l+r)>>1;
        build(ls,l,mid),build(rs,mid+1,r);
    }
    inline bool check(int a,int b,int x)
    {
        double af=Li[a].calc(x),bf=Li[b].calc(x);
        return Cmp(af,bf)?af<bf:a>b;
    }
    void modify(int p,int l,int r,int k)
    {
        int mid=(Tree[p].l+Tree[p].r)>>1;
        if(l<=Tree[p].l&&Tree[p].r<=r)
        {
            if(check(Tree[p].id,k,mid)) std::swap(Tree[p].id,k);
            if(check(Tree[p].id,k,Tree[p].l)) modify(ls,Tree[p].l,Tree[p].r,k);
            if(check(Tree[p].id,k,Tree[p].r)) modify(rs,Tree[p].l,Tree[p].r,k);
            return ;
        }
        if(l<=mid) modify(ls,l,r,k);
        if(mid<r) modify(rs,l,r,k);
    }
    inline int query(int p,int x)
    {
        if(Tree[p].l==Tree[p].r) return Tree[p].id;
        int mid=(Tree[p].l+Tree[p].r)>>1;
        int res=(x<=mid?query(ls,x):query(rs,x));
        if(check(res,Tree[p].id,x)) res=Tree[p].id;
        return res;
    }
}LcT;
inline Line getLine(double a,double b,double c,double d)
{
    if(!Cmp(a,c)) return {0,std::max(b,d),a,a};
    double k=(d-b)/(c-a);
    double e=b-(a*k);
    return {k,e,a,c};
}
int main()
{
    // freopen("lc-tree.in","r",stdin);
    // freopen("lc-tree.out","w",stdout);
    read(N);
    LcT.build(1,1,40000);
    while(N--)
    {
        int opt;read(opt);
        if(!opt)
        {
            int x;read(x);
            x=(x+lastans-1)%Mod[1]+1;
            write(lastans=LcT.query(1,x)),puts("");
        }
        else
        {
            int a,b,c,d;read(a,b,c,d);
            a=(a+lastans-1)%Mod[1]+1,b=(b+lastans-1)%Mod[2]+1;
            c=(c+lastans-1)%Mod[1]+1,d=(d+lastans-1)%Mod[2]+1;
            if(a>c) std::swap(a,c),std::swap(b,d);
            Li[++Cnt]=getLine(a,b,c,d);
            LcT.modify(1,a,c,Cnt);
        }
    }
    return 0;
}
/*
6 
1 8 5 10 8 
1 6 7 2 6 
0 2 
0 9 
1 4 7 6 7 
0 5
*/

Blue Mary

这题一眼就能转换为添加线段与单点极值的李超线段树板子，和上一道题基本一致。

不过，我还是第一次知道 std::floor() 返回的值是 double ，所以需要强制转换。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=getchar(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
const int MAXN=1e6+10;
const double eps=1e-12;
int N;
struct Line
{
    int l,r,tag;
    double k,b;
}Tree[MAXN<<2];
#define ls p<<1
#define rs p<<1|1
inline double calc(Line a,int x)
{
    return a.k*x+a.b;
}
inline int cross(Line a,Line b)
{
    return std::floor((a.b-b.b)/(b.k-a.k));
}
void build(int p,int l,int r)
{
    Tree[p]=(Line){1,50000,0,0,0};
    if(l==r) return ;
    int mid=(l+r)>>1;
    build(ls,l,mid),build(rs,mid+1,r);
}
void modify(int p,int l,int r,Line k)
{
    if(k.l<=l&&r<=k.r)
    {
        if(!Tree[p].tag) Tree[p]=k,Tree[p].tag=1;
        else if(calc(k,l)-calc(Tree[p],l)>eps&&calc(k,r)-calc(Tree[p],r)>eps) Tree[p]=k;
        else if(calc(k,l)-calc(Tree[p],l)>eps||calc(k,r)-calc(Tree[p],r)>eps)
        {
            int mid=(l+r)>>1;
            if(calc(k,mid)-calc(Tree[p],mid)>eps) std::swap(k,Tree[p]);
            if(mid-cross(k,Tree[p])>eps) modify(ls,l,mid,k);
            else modify(rs,mid+1,r,k);
        }
    }
    else
    {
        int mid=(l+r)>>1;
        if(k.l<=mid) modify(ls,l,mid,k);
        if(mid<k.r) modify(rs,mid+1,r,k);
    }
}
double query(int p,int l,int r,int k)
{
    if(l==r) return calc(Tree[p],k);
    else
    {
        int mid=(l+r)>>1;
        double ans=calc(Tree[p],k);
        if(k<=mid) return std::max(ans,query(ls,l,mid,k));
        else return std::max(ans,query(rs,mid+1,r,k));
    }
}
char opt[30];
int main()
{
    read(N);
    for(int i=1;i<=N;++i)
    {
        scanf("%s",opt);
        if(opt[0]=='P')
        {
            double s,p;scanf("%lf%lf",&s,&p);
            Line k;
            k.l=1,k.r=50000,k.k=p,k.b=s-p;
            modify(1,1,50000,k);
        }
        else
        {
            int x;read(x);
            printf("%d\n",(int)std::floor(query(1,1,50000,x)/100));
        }
    }
    return 0;
}
/*
10
Project 5.10200 0.65000
Project 2.76200 1.43000
Query 4
Query 2
Project 3.80200 1.17000
Query 2
Query 3
Query 1
Project 4.58200 0.91000
Project 5.36200 0.39000
*/
相关文章