Eternity

Until The End

跳舞链 & 十字链表

发表于 更新于 分类于 ，
本文字数： 9.8k 阅读时长 ≈ 9 分钟

优雅爆搜。

$\mathbf{D}\text{ancing }\mathbf{L}\text{inks }\mathbf{X}$ 是一种高效的数据结构，用于优化搜索。

一般可以解决精准覆盖问题和重复覆盖问题两种问题。其中重复覆盖问题需要配合迭代加深搜索（$\text{IDA}\ast$）。

精准覆盖问题

原题指路

从一个大小为 $n\times m$ 的 $01$ 矩阵中选出 $k$ 行使每一列刚好只有一个 $1$ ，其它为 $0$ 。可能无解。

$n,m\leq 500,\sum matrix\leq 5000$ ，即 $1$ 的个数不超过 $5000$ 。

考虑到有一个特殊条件是 $1$ 的个数，所以考虑对于 $1$ 的点建立结点，否则不建立，以省下时空优化爆搜。

可以先考虑直接爆搜，判断每一行取不取，并与前面所有列比较，时间复杂度 $\mathcal O(m2^n)$ ，极其不优秀的时间。

那么，我们有没有可以在多项式时间里解决这个问题的方法呢。

答案是，没有。这是一个 $\text{NP}$ 完全问题，无解。（至少现在来看）

十字链表

一个 $head$ 作为行列链的头点，初始化为：

这就是十字链表的初始化状态，那么，现在我们的矩阵中 $(1,1)$ 有一个 $1$ ，十字链表就会相应做出改变：

虽然丑，但是应该是很直观的。

然后搬一张洛谷博客上比较好看的图：

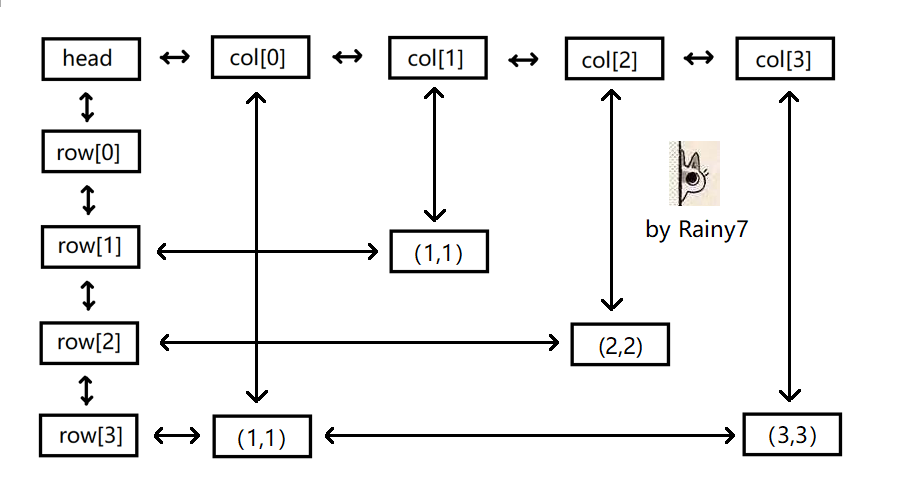
摘自「舞蹈链 $\text{DLX}$ 」学习笔记 。

参数声明

$Idx$ $ans$
当前 $1$ 的编号 答案数组
$cnt[x]$ $row[i]$ $col[i]$
第 $x$ 列里 $1$ 的个数 第 $i$ 个 $1$ 的行 第 $i$ 个 $1$ 的列
$Le[i]$ $Ri[i]$ $Up[i]$ $Do[i]$
左指针 右指针 上指针 下指针

实现

回到 $\text{DLX}$ 问题，假设当前我们现在要选择第 $x$ 行，第 $x$ 行在 $p_1,p_2,p_3$ 有 $1$ 那么显然地，我们不可能再选择包含了 $p_1,p_2,p_3$ 的行，假如有 $y_1,y_2$ ，那么，我们把 $p_1,p_2,p_3$ 列和 $y_1,y_2$ 行全部删除，并再未被删除的地方继续搜索，如果当整个矩阵都被删除的话，即表示有解。

所以，现在的问题在于，如何快速处理删除和恢复操作。这个时候十字链表就起作用了。

直接把链表指针指空即可，这里给出删除和恢复的模板，基本不变：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int Le[MAXN],Ri[MAXN],Up[MAXN],Do[MAXN];
//十字链表的左右上下指针
int Cnt[MAXN],Row[MAXN],Col[MAXN];
//链表长度，行列信息
inline void remove(int p)	//删除
{
    Ri[Le[p]]=Ri[p],Le[Ri[p]]=Le[p];
    for(int i=Do[p];i!=p;i=Do[i])
        for(int j=Ri[i];j!=i;j=Ri[j])
        {
            --Cnt[Col[j]];
            Up[Do[j]]=Up[j],Do[Up[j]]=Do[j];
        }
}
inline void recover(int p)	//恢复
{
    for(int i=Up[p];i!=p;i=Up[i])
        for(int j=Le[i];j!=i;j=Le[j])
        {
            Up[Do[j]]=j,Do[Up[j]]=j;
            ++Cnt[Col[j]];
        }
    Ri[Le[p]]=p,Le[Ri[p]]=p;
}

因为已经说过了 $\text{DLX}$ 是建立在 $1$ 上优化的，所以每次加点也只加 $1$ 。

1
2
3
4
5
6
7
inline void add(int &he,int &ta,int x,int y)
{
    Row[Idx]=x,Col[Idx]=y,++Cnt[y];
    Up[Idx]=y,Do[Idx]=Do[y],Up[Do[y]]=Idx,Do[y]=Idx;
    Ri[he]=Le[ti]=Idx,Ri[Idx]=ta,Le[Idx]=he;
    ta=Idx++;
}

可以看出，十字链表的实现就是数组套数组的实现，理解可能有些费力，可以尝试在背诵的基础上理解。

下面是爆搜函数的实现（以此题为例）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool dfs()
{
    if(!Ri[0]) return 1;
    int p=Ri[0];
    for(int i=Ri[0];i;i=Ri[i])
        	if(Cnt[i]<Cnt[p]) p=i;
    remove(p);
    for(int i=Do[p];i!=p;i=Do[i])
    {
        ans[++Top]=Row[i];
        for(int j=Ri[i];j!=i;j=Ri[j]) remove(Col[j]);
        if(dfs()) return 1;
        for(int j=Le[i];j!=i;j=Le[j]) recover(Col[j]);
        --Top;
    }
    recover(p);
    return 0;
}

爆搜有两个剪枝：

  1. 每一次选择 $1$ 个数最少的列，这样保证更有概率有解；

前面也提及过，十字链表需要初始化：

1
2
3
4
5
6
7
8
9
10
inline void init()
{
    for(re int i=0;i<=M;++i)
    {
        Le[i]=i-1,Ri[i]=i+1;
        Up[i]=Do[i]=i;
    }
    Le[0]=M,Ri[M]=0;
    Idx=M+1;
}

然后这道题基本上就完成了。说起来，关于空间的问题的话，一般而言，十字链表所需要的空间是 $\mathcal O(\max(n,m)+cnt[1])$ ，即行列数加上 $1$ 的个数，差不多。

$\textcolor{green}{Accepted}\text{ Code:}$

查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
const int MAXN=5.5e3+10;
int N,M,Idx,Top;
int Le[MAXN],Ri[MAXN],Up[MAXN],Do[MAXN];
//十字链表的左右上下指针
int Cnt[MAXN],Row[MAXN],Col[MAXN];
//链表长度，行列信息
int ans[MAXN];
inline void init()
{
    for(re int i=0;i<=M;++i)
    {
        Le[i]=i-1,Ri[i]=i+1;
        Up[i]=Do[i]=i;
    }
    Le[0]=M,Ri[M]=0;
    Idx=M+1;
}
inline void add(int &he,int &ta,int x,int y)
{
    Row[Idx]=x,Col[Idx]=y,++Cnt[y];
    Up[Idx]=y,Do[Idx]=Do[y],Up[Do[y]]=Idx,Do[y]=Idx;
    Ri[he]=Le[ta]=Idx,Ri[Idx]=ta,Le[Idx]=he;
    ta=Idx++;
}
inline void remove(int p)	//删除
{
    Ri[Le[p]]=Ri[p],Le[Ri[p]]=Le[p];
    for(re int i=Do[p];i!=p;i=Do[i])
        for(re int j=Ri[i];j!=i;j=Ri[j])
        {
            --Cnt[Col[j]];
            Up[Do[j]]=Up[j],Do[Up[j]]=Do[j];
        }
}
inline void recover(int p)	//恢复
{
    for(re int i=Up[p];i!=p;i=Up[i])
        for(re int j=Le[i];j!=i;j=Le[j])
        {
            Up[Do[j]]=j,Do[Up[j]]=j;
            ++Cnt[Col[j]];
        }
    Ri[Le[p]]=p,Le[Ri[p]]=p;
}
bool dfs()
{
    if(!Ri[0]) return 1;
    int p=Ri[0];
    for(re int i=Ri[0];i;i=Ri[i])
        	if(Cnt[i]<Cnt[p]) p=i;
    remove(p);
    for(re int i=Do[p];i!=p;i=Do[i])
    {
        ans[++Top]=Row[i];
        for(re int j=Ri[i];j!=i;j=Ri[j]) remove(Col[j]);
        if(dfs()) return 1;
        for(re int j=Le[i];j!=i;j=Le[j]) recover(Col[j]);
        --Top;
    }
    recover(p);
    return 0;
}
int main()
{
    // freopen(".in","r",stdin);
    // freopen(".out","w",stdout);
    read(N,M);
    init();
    for(re int i=1;i<=N;++i)
    {
        int he=Idx,ta=Idx;
        for(re int j=1,x;j<=M;++j)
        {
            read(x);
            if(x) add(he,ta,i,j);
        }
    }
    if(dfs())
    {
        for(re int i=1;i<=Top;++i) write(ans[i],' ');
        return 0;
    }
    else write("No Solution!");
    return 0;
}
/*
3 3
0 0 1
1 0 0
0 1 0
*/

重复覆盖问题

从一个大小为 $n\times m$ 的 $01$ 矩阵中选出 $k$ 行使每一列至少有一个 $1$ ，其它为 $0$ 。可能无解。

$n,m\leq 500,\sum matrix\leq 5000$ ，即 $1$ 的个数不超过 $5000$ 。

需要前置知识：迭代加深优先搜索 $\text{IDA}\ast$ 算法，我不会，所以先搁着。

不同于精确覆盖问题要求的是矩阵必须稀疏，重复覆盖问题发挥作用的条件在于答案不能太大，这个条件来源于其运行方式——$\text{IDA}\ast$ 。

例题

如果要用 $\text{DLX}$ 做题的话，你就不能把它当作矩阵看。——$\text{Rainy7}$

事实上，因为 $\text{DLX}$ 的时间复杂度真正与 $1$ 的个数有关，所以矩阵大小甚至可以达到 $10000$ 左右，但是，这个矩阵必须是稀疏的。

数独

其实的话，稍微给 $\operatorname{dfs}$ 减减枝都能过的。

考虑构造一个能满足要求的 $01$ 矩阵。

第 $i$ 行表示第 $i$ 个格子选哪个数，则一共有 $9^3$ 行。

列有四种内容：

  1. 每一个格子必须填一个数，$1\sim9^2$ 列；
  2. 每一行 $1\sim9$ 都必须出现，$9^2+1\sim2\times9^2$ 列；
  3. 每一列 $1\sim9$ 都必须出现，$2\times 9^2+1\sim3\times9^3$ 列；
  4. 每一个块里 $ 1\sim9$ 都必须出现，$3\times9^2+1\sim4\times9^2$ 列。

这样就可以构造一个非常非常大的 $01$ 矩阵来运行我们的 $\text{DLX}$ 惹。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
const int MAXN=2e4+10;
const int MAXC=10;
int M=9*9*4;
int Le[MAXN],Ri[MAXN],Up[MAXN],Do[MAXN];
int Cnt[MAXN],Col[MAXN],Row[MAXN],Idx;
int ans[MAXN],Top;
struct Operation
{
    int x,y,c;
}Op[MAXN];
int G[MAXC][MAXC];
inline void init()
{
    for(int i=0;i<=M;++i)
    {
        Le[i]=i-1,Ri[i]=i+1;
        Cnt[i]=0,Do[i]=Up[i]=i;
    }
    Le[0]=M,Ri[M]=0;
    Idx=M+1;
}
inline void add(int &he,int &ta,int x,int y)
{
    Row[Idx]=x,Col[Idx]=y,++Cnt[y];
    Up[Idx]=y,Do[Idx]=Do[y],Up[Do[y]]=Idx,Do[y]=Idx;
    Ri[he]=Le[ta]=Idx,Ri[Idx]=ta,Le[Idx]=he;
    ta=Idx++;
}
inline void remove(int p)	//删除
{
    Ri[Le[p]]=Ri[p],Le[Ri[p]]=Le[p];
    for(int i=Do[p];i!=p;i=Do[i])
        for(int j=Ri[i];j!=i;j=Ri[j])
        {
            --Cnt[Col[j]];
            Up[Do[j]]=Up[j],Do[Up[j]]=Do[j];
        }
}
inline void recover(int p)	//恢复
{
    for(int i=Up[p];i!=p;i=Up[i])
        for(int j=Le[i];j!=i;j=Le[j])
        {
            Up[Do[j]]=j,Do[Up[j]]=j;
            ++Cnt[Col[j]];
        }
    Ri[Le[p]]=p,Le[Ri[p]]=p;
}
bool dfs()
{
    if(!Ri[0]) return 1;
    int p=Ri[0];
    for(int i=Ri[0];i;i=Ri[i])
        	if(Cnt[i]<Cnt[p]) p=i;
    remove(p);
    for(int i=Do[p];i!=p;i=Do[i])
    {
        ans[++Top]=Row[i];
        for(int j=Ri[i];j!=i;j=Ri[j]) remove(Col[j]);
        if(dfs()) return 1;
        for(int j=Le[i];j!=i;j=Le[j]) recover(Col[j]);
        --Top;
    }
    recover(p);
    return 0;
}
int Test;
int main()
{
    // freopen(".in","r",stdin);
    // freopen(".out","w",stdout);
    for(int i=0;i<9;++i)
        for(int j=0;j<9;++j)
            read(G[i][j]),--G[i][j];
    init();
    for(int i=0,N=1;i<9;++i)
        for(int j=0;j<9;++j)
        {
            int a=0,b=8;
            if(G[i][j]!=-1) a=b=G[i][j];
            for(int k=a;k<=b;++k,++N)
            {
                int hd=Idx,tl=Idx;
                Op[N]={i,j,k};
                add(hd,tl,N,i*9+j+1);
                add(hd,tl,N,81+i*9+k+1);
                add(hd,tl,N,81*2+j*9+k+1);
                add(hd,tl,N,81*3+(i/3*3+j/3)*9+k+1);
            }
        }
    dfs();
    for(int i=1;i<=Top;++i)
    {
        auto t=Op[ans[i]];
        G[t.x][t.y]=t.c;
    }
    for(int i=0;i<9;++i)
    {
        for(int j=0;j<9;++j) write(G[i][j]+1,' ');
        puts("");
    }
    return 0;
}
/*
8 0 0 0 0 0 0 0 0 
0 0 3 6 0 0 0 0 0 
0 7 0 0 9 0 2 0 0 
0 5 0 0 0 7 0 0 0 
0 0 0 0 4 5 7 0 0 
0 0 0 1 0 0 0 3 0 
0 0 1 0 0 0 0 6 8 
0 0 8 5 0 0 0 1 0 
0 9 0 0 0 0 4 0 0
*/

八皇后

超级数独

黑色的双倍经验。

所谓的超级数独，其实就是十六进制的数独。

如数独题类似，构造四种情况的 $01$ 矩阵，然后得到需要的方式即可。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
const int MAXN=2e4+10;
const int MAXC=20;
int M=16*16*4;
int Le[MAXN],Ri[MAXN],Up[MAXN],Do[MAXN];
int Cnt[MAXN],Col[MAXN],Row[MAXN],Idx;
int ans[MAXN],Top;
struct Operation
{
    int x,y;
    char c;
}Op[MAXN];
char G[MAXC][MAXC];
inline void init()
{
    for(int i=0;i<=M;++i)
    {
        Le[i]=i-1,Ri[i]=i+1;
        Cnt[i]=0,Do[i]=Up[i]=i;
    }
    Le[0]=M,Ri[M]=0;
    Idx=M+1;
}
inline void add(int &he,int &ta,int x,int y)
{
    Row[Idx]=x,Col[Idx]=y,++Cnt[y];
    Up[Idx]=y,Do[Idx]=Do[y],Up[Do[y]]=Idx,Do[y]=Idx;
    Ri[he]=Le[ta]=Idx,Ri[Idx]=ta,Le[Idx]=he;
    ta=Idx++;
}
inline void remove(int p)	//删除
{
    Ri[Le[p]]=Ri[p],Le[Ri[p]]=Le[p];
    for(re int i=Do[p];i!=p;i=Do[i])
        for(re int j=Ri[i];j!=i;j=Ri[j])
        {
            --Cnt[Col[j]];
            Up[Do[j]]=Up[j],Do[Up[j]]=Do[j];
        }
}
inline void recover(int p)	//恢复
{
    for(re int i=Up[p];i!=p;i=Up[i])
        for(re int j=Le[i];j!=i;j=Le[j])
        {
            Up[Do[j]]=j,Do[Up[j]]=j;
            ++Cnt[Col[j]];
        }
    Ri[Le[p]]=p,Le[Ri[p]]=p;
}
bool dfs()
{
    if(!Ri[0]) return 1;
    int p=Ri[0];
    for(re int i=Ri[0];i;i=Ri[i])
        	if(Cnt[i]<Cnt[p]) p=i;
    remove(p);
    for(re int i=Do[p];i!=p;i=Do[i])
    {
        ans[++Top]=Row[i];
        for(re int j=Ri[i];j!=i;j=Ri[j]) remove(Col[j]);
        if(dfs()) return 1;
        for(re int j=Le[i];j!=i;j=Le[j]) recover(Col[j]);
        --Top;
    }
    recover(p);
    return 0;
}
int Test;
int main()
{
    // freopen(".in","r",stdin);
    // freopen(".out","w",stdout);
    read(Test);
    while(Test--)
    {
        for(int i=0;i<16;++i) scanf("%s",G[i]);
        init();
        for(int i=0,N=1;i<16;++i)
            for(int j=0;j<16;++j)
            {
                int a=0,b=15;
                if(G[i][j]!='-') a=b=G[i][j]-'A';
                for(int k=a;k<=b;++k,++N)
                {
                    int hd=Idx,tl=Idx;
                    Op[N]={i,j,char(k+'A')};
                    add(hd,tl,N,i*16+j+1);
                    add(hd,tl,N,256+i*16+k+1);
                    add(hd,tl,N,256*2+j*16+k+1);
                    add(hd,tl,N,256*3+(i/4*4+j/4)*16+k+1);
                }
            }
        dfs();
        for(int i=1;i<=Top;++i)
        {
            auto t=Op[ans[i]];
            G[t.x][t.y]=t.c;
        }
        for(int i=0;i<16;++i) puts(G[i]);
        puts("");
    }
    return 0;
}
/*
1
--A----C-----O-I 
-J--A-B-P-CGF-H-
--D--F-I-E----P-
-G-EL-H----M-J--
----E----C--G---
-I--K-GA-B---E-J 
D-GP--J-F----A--
-E---C-B--DP--O-
E--F-M--D--L-K-A 
-C--------O-I-L-
H-P-C--F-A--B---
---G-OD---J----H 
K---J----H-A-P-L 
--B--P--E--K--A-
-H--B--K--FI-C--
--F---C--D--H-N-
*/
相关文章