Eternity

Until The End

计算几何

发表于 更新于 分类于 ，
本文字数： 13k 阅读时长 ≈ 12 分钟

“平面的向量交错生长，织成，忧伤的网。——《膜你抄》”

浮点数 x 定点数

定点数详解。

浮点数详解。

总而言之，浮点数表示为：

1
V=(-1)^S*M*R^E

其中各个变量的含义如下：

  • S：符号位，取值 $0$ 或 $1$，决定一个数字的符号，$0$ 表示正，$1$ 表示负
  • M：尾数，用小数表示，例如前面所看到的 $8.345 \times 10^0$，$8.345$ 就是尾数
  • R：基数，表示十进制数 $R$ 就是 $10$，表示二进制数 $R$ 就是 $2$
  • E：指数，用整数表示，例如前面看到的 $10^{-1}$，$-1$ 即是指数

精度处理

一般来说，计算机中存储一个数采用的是二进制，一个 $n$ 位整数将被表示为：

$x = \sum_{i = 0}^{n - 1} v_i \times 2^{i}$

如果是小数，上述公式仍然适用，只是将 $i$ 的范围由 $\mathbb{N}$ 扩大至 $\mathbb{Z}$，但由于 $2$ 的幂与 $10$ 的幂不同，一些 $10$ 进制下的有限小数会变成无限小数，而计算机能够存储的东西是有限的，因此得到的浮点数只是一个近似值。因此，在做有关浮点数的操作时，一定要考虑精度问题。

处理浮点数的精度问题

定义精度，EPS 指希腊字母 $\epsilon$：

1
const double EPS = 1e-4;

比较大小，求一个数的正负时要考虑在精度范围内认为两个数相等：

1
2
3
4
5
6
7
8
9
10
11
12
int sign(double x)
{
    if(std::fabs(x)<EPS) return 0;
    if(x<0) return -1;
    return 1;
}
int comp(double x,double y)
{
    if(std::fabs(x-y)<EPS) return 0;
    if(x<y) return -1;
    return 1;
}

向量

表示

一般而言，将一个向量表示成一个坐标，如 $t=\left(^3_2\right)$ ，则表示一个向量的起点为 $(0,0)$ ，终点是 $(3,2)$ 。如图：

img

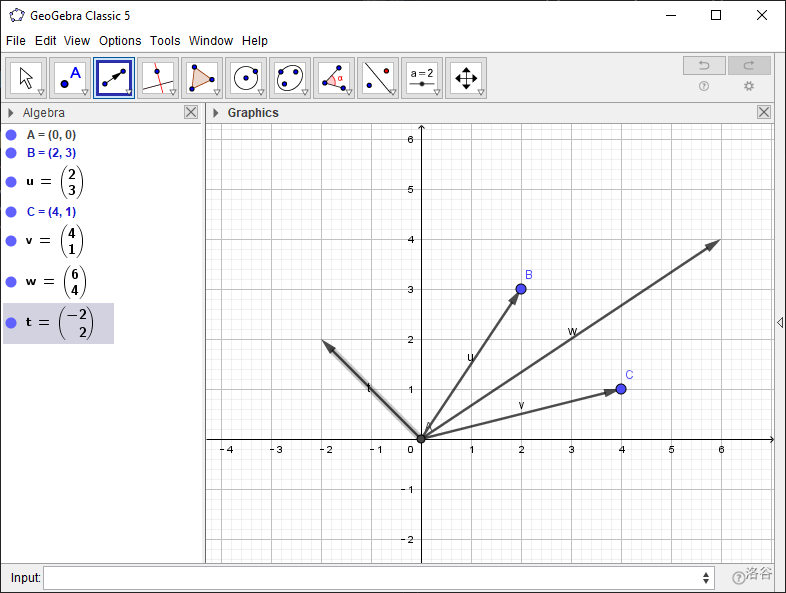
加减法则

直接加减即可，对于向量 $a=\left(^{x_1}_{y_1}\right),b=\left(^{x_2}_{y_2}\right)$ 有：

$\vec a\pm \vec b=(x_1\pm x_2,y_1\pm y_2)$

乘除法则

数乘

指的是一个实数（标量）乘上一个向量，即将该向量延长该实数倍即可。

点乘

$\vec a\cdot\vec b=|\vec a||\vec b|\cos \theta$ 。

$(x_1,y_1)\cdot(x_2,y_2)=x_1x_2+y_1y_2$

几何意义：$\vec a$ 在 $\vec b$ 上的投影长度与 $\vec b$ 的长度的积。

叉乘

不满足交换律，满足结合律。

$|\vec a\times\vec b|=|\vec a||\vec b|\sin\theta$

$\vec a\times\vec b=-(\vec b\times\vec a)$

坐标表示：$(x_1,y_1)\times(x_2,y_2)=x_1y_2-x_2y_1$

几何意义：$\vec{a}$ 与 $\vec{b}$ 形成的平行四边形的有向面积（$\theta$ 带符号），$\vec{a}$ 逆时针转到 $\vec{b}$ 为正。

代码实现(风格指导Rusun)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//重载运算符实现
struct Vector
{
    double x,y;		//用坐标表示向量
    Vector operator+(Vector a)
    {
        return (Vector){x+a.x,y+a.y};
	}	//加法
    Vector operator-(const Vector &a)const
    {
        return (Vector){x-a.x,y-a.y}
    }	//减法，那2个const和那个&都是卡常用的。
    Vector operator*(const double &a)const
    {
        return (Vector){x*a,y*a};
    }	//数乘
    Vector operator/(const double &a)const
    {
        return(Vector){x/a,y/a};
    }
    double operator^(const Vector &a)const
    {
        return x*a.x+y*a.y;
	}	//点乘
    double operator&(const Vector &a)const
    {
        return x*a.y-a.x*y;
    }	//叉乘
}

代码实现(风格指导PigAunt)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//用函数实现
struct Point
{
    double x,y;
    /*
    	省略加减和数乘。
    */
    double dot(Point a,Point b)
    {
        return a.x*b.x+a.y*b.y;
    }	//点积
    double cross(Point a,Point b)
    {
		return a.x*b.y-a.y*b.x;
    }	//叉积
    double getLength(Point a)
    {
		return sqrt(dot(a,a));
    }	//取模
    	//因为a·a=|a|^2，所以会这样。
    double getAngle(Point a,Point b)
    {
        return acos(dot(a,b)/getLength(a)/getLength(b));
    }	//计算向量夹角
    	//a·b=|a||b|sinx
    	//x=arccos(a·b/(|a||b|))
    double area(Point a,Point b,Point c)
    {
        return cross(b-a,c-a);
    }	//求向量构成的平行四边形有向面积（分正负）
}

点与直线

直线表达

  1. 点斜式：$ax+by+c=0$
  2. 点向式：$p_0+vt$
  3. 斜截式：$y=kx+b$

点向式中，$p=(x_0,y_0)$ 是直线上的一个点，而 $v=\left(^{x_v}_{y_v}\right)$ 是该直线上的一个向量，那么这个直线上的任意一个点都可以用 $p+vt,t\in \mathbb R$ 表示。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct Point
{
    double x,y;
	/*
		沿用PigAunt的代码风格
	*/
    //假设一条直线AB，判断点C是否在AB上，则有ACxBC=0
    Point getLineIntersection(Point p,Vector v,Point q,Vector w)
    {
        Vector u=p-q;
        double t=cross(w,u)/cross(v,w);
        return p+v*t;
    }//求直线交点，cross(v,w)=0则两直线平行（重合）。
    
}

凸包

最小周长值

对于一大堆点，我们需要确定一个多边形，使所有点都在多边形内（可以在边上），使得这个多边形周长最短，这就是这个凸包。凸包的应用典型就是斜率优化

Andrew 算法

先给所有点以 $x$ 为第一关键字，$y$ 为第二关键字从小到大排序；然后扫描每个点，看这个点加入后能不能打破原来凸包的性质，如果能，就把原来的点删了；然后将新的点加入。从左往右做一次，我们得到一个上凸壳；从右往左再做一次，我们就得到了一个凸包（已加入的点不再加入），使用向量叉积判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
inline void andrew()
{
    std::sort(p+1,p+1+cnt);
    int top=0;
    for(int i=1;i<=cnt;++i)
    {
        while(top>=2&&area(p[stk[top-1]],p[stk[top]],p[i])<=0)
        {
            if(area(p[stk[top-1]],p[stk[top]],p[i])<0) use[stk[top--]]=0;
            else --top;
        }
        stk[++top]=i;
        use[i]=1;
    }
    use[1]=0;
    for(int i=cnt;i>=1;--i)
    {
        if(use[i]) continue;
        while(top>=2&&area(p[stk[top-1]],p[stk[top]],p[i])<0) --top;
        	//这里不能取0，是为了应对共线的情况。
        stk[++top]=i;
    }
}

练习

洛谷信用卡凸包

就类似于小学做过的一类题，一个多边形周长加上一个圆的周长。将题目给出的数据转化为定点，然后就是凸包的裸题了。补充一个向量旋转的公式：

1
2
3
4
inline Point rotate(Point a,double alph)
{
    return {a.x*cos(alph)+a.y*sin(alph),-a.x*sin(alph)+a.y*cos(alph)};
}

Talk isn’t cheap,don’t show me the Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
#define db double
typedef long long ll;
using namespace std;
const int MAXN=4e4+1;
const int dx[]={0,1,-1,1,-1};
const int dy[]={0,1,1,-1,-1};
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
int N,cnt;
double len,wid,rth;
struct Point
{
    double x,y;
    Point operator-(const Point &a)const
    {
        return {x-a.x,y-a.y};
    }
    Point(double x=0,double y=0):x(x),y(y){}
}Pt[MAXN],centre[MAXN];
inline double cross(Point a,Point b)
{
    return a.x*b.y-a.y*b.x;
}
inline double area(Point a,Point b,Point c)
{
    return cross(b-a,c-a);
}
inline Point rotate(Point a,double alph)
{
    return {a.x*cos(alph)+a.y*sin(alph),-a.x*sin(alph)+a.y*cos(alph)};
}
double theta[MAXN];
inline void init()
{
    for(int i=1;i<=N;++i)
        for(int k=1;k<=4;++k)
        {
            Point dis=rotate({dx[k]*len,dy[k]*wid},-theta[i]);
            Pt[++cnt]=Point(centre[i].x+dis.x,centre[i].y+dis.y);
        }
    // for(int i=1;i<=cnt;++i) printf("%.2lf %.2lf\n",Pt[i].x,Pt[i].y);
}
int stk[MAXN<<1],top;
bool used[MAXN];
inline bool cmp(Point a,Point b)
{
    if(a.x==b.x) return a.y<b.y;
    return a.x<b.x;
}
inline double getDist(Point a,Point b)
{
    return std::sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
inline void andrew()
{
    std::sort(Pt+1,Pt+1+cnt,cmp);
    top=0;
    for(int i=1;i<=cnt;++i)
    {
        while(top>=2)
        {
            double res=area(Pt[stk[top-1]],Pt[stk[top]],Pt[i]);
            if(res<0) used[stk[top--]]=0;
            else if(res==0) --top;
            else break;
        }
        stk[++top]=i;
        used[i]=1;
    }
    used[1]=0;
    for(int i=cnt;i>=1;--i)
    {
        if(used[i]) continue;
        while(top>=2&&area(Pt[stk[top-1]],Pt[stk[top]],Pt[i])<0) --top;
        stk[++top]=i;
    }
    double res=0;
    for(int i=2;i<=top;++i) res+=getDist(Pt[stk[i-1]],Pt[stk[i]]);
    printf("%.2lf",res+(2*rth*acos(-1)));
}
int main()
{
    // freopen("geo.in","r",stdin);
    // freopen("geo.out","w",stdout);
    read(N);
    scanf("%lf%lf%lf",&wid,&len,&rth);
    wid=(wid-2*rth)/2;
    len=(len-2*rth)/2;
    for(int i=1;i<=N;++i) scanf("%lf%lf%lf",&centre[i].x,&centre[i].y,&theta[i]);
    init();
    andrew();
    return 0;
}
/*
2
6.0 2.0 0.0
0.0 0.0 0.0
2.0 -2.0 1.5707963268
*/

旋转卡壳

这玩意儿居然有 $2\times2\times2\times3=24$ 种读法。

正确读法：$\text{旋}(xu\acute{a}n)\text{转}(zhu\grave an)\text{卡}(qi\check a)\text{壳}(qi\grave ao)$

定义

对于一个凸包，其直径则是该凸包内两点的最大距离。可以证明：这两个点必定在凸包上（边上）。旋转卡壳则是一种求凸包直径的算法。

那么，为什么会叫旋转卡壳呢？

扩句：

用两条互相平行的直线进行（旋转）并（卡）住凸包形成对踵点的（壳）并计算。

所谓对踵点，就是一组点是当前这两条直线卡住凸包（与凸包相切）的那两个点组成的点对，则是一组对踵点。（可以证明，对于任意一个点，与其组成对踵点的点不超过 $3$ 个，那么对踵点不会超过 $3n$ 个，对踵点对也就不会超过 $\frac{3n}{2}$ 个）

img

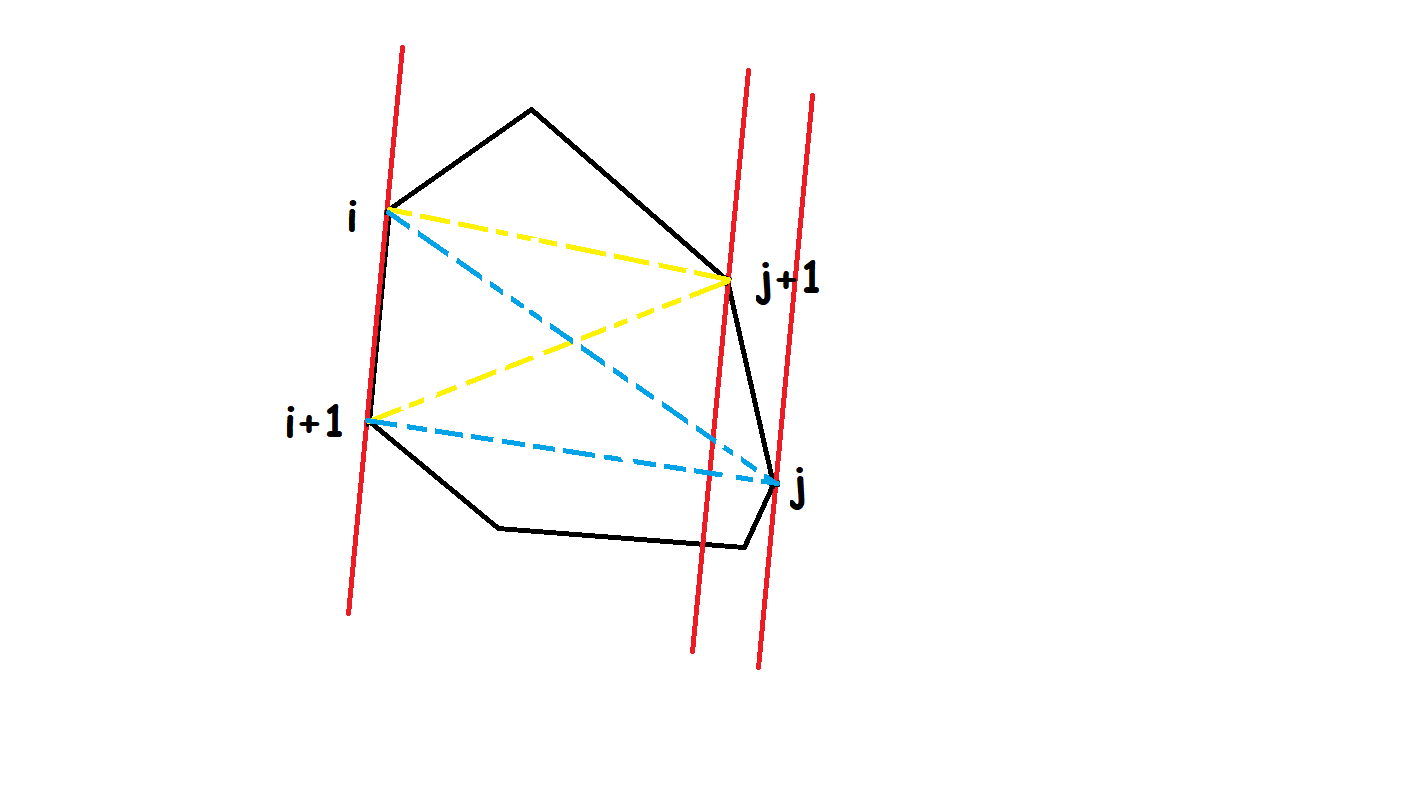
计算

实际上，因为角度是一个区间，内有无数个数，所以让计算机去模拟旋转是不可能的，只会 $TLE$ 到飞起。而我们也会发现，真正有效的只会是当一条旋转直线与凸包的某条边平行时，才会去计算，所谓的旋转卡壳，实际上只是让人脑能够理解罢了。

img

首先使用任何一种凸包算法求出给定所有点的凸包，有着最长距离的点对一定在凸包上。而由于凸包的形状，我们发现，逆时针地遍历凸包上的边，对于每条边都找到离这条边最远的点，那么这时随着边的转动，对应的最远点也在逆时针旋转，不会有反向的情况，这意味着我们可以在逆时针枚举凸包上的边时，记录并维护一个当前最远点，并不断计算、更新答案。

求出凸包后的数组自然地是按照逆时针旋转的顺序排列，不过要记得提前将最左下角的 $1$ 节点补到数组最后，这样在挨个枚举边 $(i,i+1)$ 时，才能把所有边都枚举到。

枚举过程中，对于每条边，都检查 $j+1$ 和边 $(i,i+1)$ 的距离是不是比 更大，如果是就将 加一，否则说明 是此边的最优点。判断点到边的距离大小时可以用叉积分别算出两个三角形的面积（如图，黄、蓝两个同底三角形的面积）并直接比较。

注意：

作为一个数组下标喜欢使用 $[1,n]$ 的人，也必须做出取舍，在凸包和旋转卡壳中，使用 $[0,n-1]$ 有几个好处。

  1. 对于单调栈之间，我们会统计两次起点，所以 top 的值会达到 $n+1$ ，则会 $RE$ ，显然。
  2. 在旋转卡壳中有一个操作会执行 j=(j+1)%top ，这样的话，如果单调栈的下标是在 $[0,top-1]$ 的话，就直接执行，而如果是 $[1,top]$ 的话，模就会模出问题。
1
2
3
4
5
6
7
8
9
10
11
12
inline double rotcal()
{
    if(top<=2) return getDist(Pt[0],Pt[N-1]);
    double res=0;
    for(int i=0,j=2;i<top;++i)
    {
        Pir a=Pt[stk[i]],b=Pt[stk[i+1]];
        while(area(a,b,Pt[stk[j]])<area(a,b,Pt[stk[j+1]])) j=(j+1>=top?0:j+1);
        res=max(res,max(getDist(a,Pt[stk[j]]),getDist(b,Pt[stk[j]])));
    }
    return res;
}

把旋转卡壳理解为当枚举边的时候，距离边最远的点是单调的。

凸包时间复杂度 $\mathcal O(n\log n)$ ，旋转卡壳时间复杂度 $\mathcal O(n)$ ，总时间复杂度 $\mathcal O(n\log n)$ 。

以 $0$ 为起点的旋转卡壳代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int stk[MAXN<<1],top;
bool use[MAXN];
inline void andrew()
{
    std::sort(Pt,Pt+N);
    top=0;
    for(int i=0;i<N;++i)
    {
        while(top>=2&&area(Pt[stk[top-2]],Pt[stk[top-1]],Pt[i])<=0)
        {
            if(area(Pt[stk[top-2]],Pt[stk[top-1]],Pt[i])<0)
                use[stk[--top]]=0;
            else --top;
        }
        stk[top++]=i;
        use[i]=1;
    }
    use[0]=0;
    for(int i=N-1;i>=0;--i)
    {
        if(use[i]) continue;
        while(top>=2&&area(Pt[stk[top-2]],Pt[stk[top-1]],Pt[i])<=0)
            --top;
        stk[top++]=i;
    }
    --top;
}
inline double rotcal()
{
    if(top<=2) return getDist(Pt[0],Pt[N-1]);
    double res=0;
    for(int i=0,j=2;i<top;++i)
    {
        Pir a=Pt[stk[i]],b=Pt[stk[i+1]];
        while(area(a,b,Pt[stk[j]])<area(a,b,Pt[stk[j+1]])) j=(j+1>=top?0:j+1);
        res=max(res,max(getDist(a,Pt[stk[j]]),getDist(b,Pt[stk[j]])));
    }
    return res;
}

某谷模板题

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
#define db double
typedef long long ll;
using namespace std;
const int MAXN=5e4+1;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
int N;
using Pir=std::pair<double,double>;
#define fi first
#define se second
Pir Pt[MAXN];
Pir operator-(Pir &a,Pir &b)
{
    return make_pair(a.fi-b.fi,a.se-b.se);
}
inline double cross(Pir a,Pir b)
{
    return a.fi*b.se-b.fi*a.se;
}
inline double area(Pir a,Pir b,Pir c)
{
    return cross(b-a,c-a);
}
inline double getDist(Pir a,Pir b)
{
    return (a.fi-b.fi)*(a.fi-b.fi)+(a.se-b.se)*(a.se-b.se);
}
int stk[MAXN<<1],top;
bool use[MAXN];
inline void andrew()
{
    std::sort(Pt,Pt+N);
    top=0;
    for(int i=0;i<N;++i)
    {
        while(top>=2&&area(Pt[stk[top-2]],Pt[stk[top-1]],Pt[i])<=0)
        {
            if(area(Pt[stk[top-2]],Pt[stk[top-1]],Pt[i])<0)
                use[stk[--top]]=0;
            else --top;
        }
        stk[top++]=i;
        use[i]=1;
    }
    use[0]=0;
    for(int i=N-1;i>=0;--i)
    {
        if(use[i]) continue;
        while(top>=2&&area(Pt[stk[top-2]],Pt[stk[top-1]],Pt[i])<=0)
            --top;
        stk[top++]=i;
    }
    --top;
}
inline double rotcal()
{
    if(top<=2) return getDist(Pt[0],Pt[N-1]);
    double res=0;
    for(int i=0,j=2;i<top;++i)
    {
        Pir a=Pt[stk[i]],b=Pt[stk[i+1]];
        while(area(a,b,Pt[stk[j]])<area(a,b,Pt[stk[j+1]])) j=(j+1>=top?0:j+1);
        res=max(res,max(getDist(a,Pt[stk[j]]),getDist(b,Pt[stk[j]])));
    }
    return res;
}
int main()
{
    // freopen("geo.in","r",stdin);
    // freopen("geo.out","w",stdout);
    read(N);
    for(re int i=0;i<N;++i) scanf("%lf%lf",&Pt[i].fi,&Pt[i].se);
    andrew();
    printf("%.0lf",rotcal());
    return 0;
}
/*
4
0 0
0 1
1 1
1 0
*/

三角剖分

将一个 $n$ 边形剖分成 $n-2$ 个不相交的三角形，这是从小学说到高中的数学题了。

参考了 $Dyd$ 的 $Blog$

对于一个圆和一个三角形的面积交，则会分成四种情况（读者可以自行模拟）：

  1. 圆把三角形包住，则面积交就是三角形面积；
  2. 有 $1$ 个点在圆外，则面积是一个小三角形面积和一个小扇形的面积和；
  3. 有 $2$ 个点在圆外且其边与圆相离，则面积是一个扇形；
  4. 有 $2$ 个点在圆外且其边与圆相割，则面积是 $2$ 个小扇形加上一个三角形的面积和。

但是，多边形与圆面积交呢？情况繁杂，所以把这个多边形分成很多个三角形来算也行。

叉积运用：多边形面积分

对于一个多边形的面积（知道所有点的坐标），最好的方法是怎么算？

平面上任取一点 $p$ ，画出 $p$ 与多边形顶点的向量，则 $S=\sum_{I,J\in N}\vec{PI}\times\vec{PJ}$ ，如果点 $P$ 在多边形内很好证明，但是在多边形外也是成立的，因为叉积的结果是有向的，所以当把所有和全部算完，会发现正好会把多余部分减去，这个方法同样适用于凹多边形，读者可以自行探取。

扫描线

矩形面积并

线段树进阶知识，详见扫描线

img

三角面积并

三角形并不会平行于平面直角坐标系，那么我们用一条 $y$ 轴线，只要有顶点（或者交点）就划一次，全部划分，然后按照梯形（广义）面积来算。时间复杂度是 $\mathcal O(n^3)$ 。

听起来很简单，但是实施在代码上实际上十分困难。有很多需要讲的点。先咕着（还没学懂）。

辛普森积分

自适应辛普森积分

圆的面积并

平面最近点对

智慧法

我们充分发扬人类智慧

正解分治，跟我使用智慧法有什么关系？

在平面最近点对（加强版）里最高赞题解写道：

“我们充分发扬人类智慧：
将所有点全部绕原点旋转同一个角度，然后按 $x$ 坐标排序根据数学直觉，在随机旋转后，答案中的两个点在数组中肯定不会离得太远
所以我们只取每个点向后的 $5$ 个点来计算答案这样速度快得飞起，在 $n=10^6$时都可以在 $1s$ 内卡过”

这开启了智慧法过本问题（恶心出题人）的新时代！

Solution

相关文章