Eternity

Until The End

平衡树

发表于 更新于 分类于 ，
本文字数： 25k 阅读时长 ≈ 23 分钟

“平衡的旋转，亦是世上最美的舞蹈。”

二叉搜索树(Binary Search Tree)

定义

顾名思义，一棵二叉树，满足左子点的值小于父节点，右子点的值大于父节点。所有节点都满足该性质。当然，空节点不算。

性质/特点

能够高效地完成：

  • 插入
  • 查询
  • 删除

若 $x$ 是其中节点，而 $y$ 和 $z$ 分别是其左子点与右子点。那么它们满足：

$y.key \leq x.key \leq z.key$

复杂度/代码实现

均摊 $O(\log n)$ 。

查找

从根节点开始，按性质向下查找即可

插入

根据性质查找直到空节点，并新建节点。

删除

叶节点

直接删除

仅有一个子节点的父节点

上移其子节点，删除其本身

双子节点的父节点

找到需要删除的节点 $p$ 的直接前驱（或后驱） $s$ ，用 $s$ 代替 $p$ ，并删除 $s$

另话

然而，二叉查找树虽然均摊 $O(\log n)$ ，但实际上，当树作为一条链时，其任何操作都是 $O(n)$ ，那做个P啊，所以就会有了平衡树这种东西。

Treap

有两位巨佬告诉我， $\text{Treap}$ 这东西不需要学。所以我也就简单提提。

实现

$Treap$ 实际上是一个合成词，$Tree+Heap$ 的合成。也顾名思义，给每一个节点加入一个随机值 $rand()$ 以达到堆性质而使其基本达到平衡。从而保证树的深度在 $\log n$ 左右。当这棵树的深度达到平衡极限时，进行左旋和右旋操作使深度降低。

旋转(rotate)

旋转分为左旋(zig)和右旋(zag)。其目的是使子节点转到根节点处。因为平衡树的操作众多，所以这里重点讲旋转，其他的因题而异即可。

$rotate(\&p,d)$ 中，以 $p$ 为初始根节点旋转，$d=0$ 时左旋，$d=1$ 时右旋。

1
2
3
4
5
6
7
8
9
10
inline void underRotate(int &p,int d)
{
	int k=Tree.son[p][d^1];
	Tree.son[p][d^1]=Tree.son[k][d];
	Tree.son[k][d]=p;
	underPushUp(p);
	underPushUp(k);
	p=k;
	return ;
}

以左旋为例：

将右子点保存为 $k$ ，将 $p$ 的右子点变成 $k$ 的左子点。再将 $k$ 的左子点变成 $p$ 。然后将 $p$ 和 $k$ 都进行 $pushup$ 。（如果你不知道 $pushup$ 是啥请看线段树学习笔记。

初始化

建立一个极小点($-\inf$)和一个极大点($\inf$)防止越界

AC Code

查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define underMax(x,y) ((x)>(y)?(x):(y))
#define underMin(x,y) ((x)<(y)?(x):(y))
typedef long long ll;
using namespace std;
const int MAXN=1e6+1;
const int INF=0x7f7f7f7f;
template<class T>
inline void underRead(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
int M,Idx,Rt,op,x;
struct Treap
{
    int son[2],val,rd,cnt,size;
}Tree[MAXN];
inline int underNew(int val)
{
    Tree[++Idx].val=val;
    Tree[Idx].rd=rand();
    Tree[Idx].cnt=Tree[Idx].size=1;
    return Idx;
}
inline void underPushUp(int p)
{
    Tree[p].size=Tree[Tree[p].son[0]].size+Tree[Tree[p].son[1]].size+Tree[p].cnt;
}
inline void underBuild()
{
    underNew(-INF),underNew(INF);
    Rt=1,Tree[1].son[1]=2;
    underPushUp(Rt);
}
inline void underRotate(int &p,int d)
{
    int k=Tree[p].son[d^1];
    Tree[p].son[d^1]=Tree[k].son[d];
    Tree[k].son[d]=p;
    p=k;
    underPushUp(Tree[p].son[d]);
    underPushUp(p);
	return ;
}   //d=0 -> zag
    //d=1 -> zig
inline void underInsert(int &p,int val)
{
    if(p==0)
    {
        p=underNew(val);
        return ;
    }
    if(val==Tree[p].val)
    {
        ++Tree[p].cnt,underPushUp(p);
        return ;
    }
    if(val<Tree[p].val)
    {
        underInsert(Tree[p].son[0],val);
        if(Tree[p].rd<Tree[Tree[p].son[0]].rd) underRotate(p,1);
    }
    else
    {
        underInsert(Tree[p].son[1],val);
        if(Tree[p].rd<Tree[Tree[p].son[1]].rd) underRotate(p,0);
    }
    underPushUp(p);
}
inline int underGetRankByVal(int p,int val)
{
    if(p==0) return 0;
    if(val==Tree[p].val) return Tree[Tree[p].son[0]].size+1;
    if(val<Tree[p].val) return underGetRankByVal(Tree[p].son[0],val);
    return underGetRankByVal(Tree[p].son[1],val)+Tree[Tree[p].son[0]].size+Tree[p].cnt;
}
inline int underGetValByRank(int p,int rank)
{
    if(p==0) return INF;
    if(Tree[Tree[p].son[0]].size>=rank) return underGetValByRank(Tree[p].son[0],rank);
    if(Tree[Tree[p].son[0]].size+Tree[p].cnt>=rank) return Tree[p].val;
    return underGetValByRank(Tree[p].son[1],rank-Tree[Tree[p].son[0]].size-Tree[p].cnt);
}
inline int underGetPre(int val)
{
    int ans=1,p=Rt;
    while(p)
    {
        if(val==Tree[p].val)
        {
            if(Tree[p].son[0])
            {
                p=Tree[p].son[0];
                while(Tree[p].son[1]) p=Tree[p].son[1];
                ans=p;
            }
            break;
        }
        if(Tree[p].val<val&&Tree[p].val>Tree[ans].val) ans=p;
        p=(val<Tree[p].val?Tree[p].son[0]:Tree[p].son[1]);
    }
    return Tree[ans].val;
}
inline int underGetNxt(int val)
{
    int ans=2,p=Rt;
    while(p)
    {
        if(val==Tree[p].val)
        {
            if(Tree[p].son[1])
            {
                p=Tree[p].son[1];
                while(Tree[p].son[0]) p=Tree[p].son[0];
                ans=p;
            }
            break;
        }
        if(Tree[p].val>val&&Tree[p].val<Tree[ans].val) ans=p;
        p=(val<Tree[p].val?Tree[p].son[0]:Tree[p].son[1]);
    }
    return Tree[ans].val;
}
inline void underErase(int &p,int val)
{
    if(p==0) return ;
    if(val==Tree[p].val)
    {
        if(Tree[p].cnt>1)
        {
            --Tree[p].cnt,underPushUp(p);
            return ;
        }
        if(Tree[p].son[0]||Tree[p].son[1])
        {
            if(!Tree[p].son[1]||Tree[Tree[p].son[0]].rd>Tree[Tree[p].son[1]].rd) underRotate(p,1),underErase(Tree[p].son[1],val);
            else underRotate(p,0),underErase(Tree[p].son[0],val);
            underPushUp(p);
        }
        else p=0;
        return ;
    }
    val<Tree[p].val?underErase(Tree[p].son[0],val):underErase(Tree[p].son[1],val);
    underPushUp(p);
}
int main()
{
    // freopen("splay.in","r",stdin);
    // freopen("splay.out","w",stdout);
    underBuild();
    underRead(M);
    while(M--)
    {
        underRead(op),underRead(x);
        switch(op)
        {
            case 1:underInsert(Rt,x);break;
            case 2:underErase(Rt,x);break;
            case 3:printf("%d\n",underGetRankByVal(Rt,x)-1);break;
            case 4:printf("%d\n",underGetValByRank(Rt,x+1));break;
            case 5:printf("%d\n",underGetPre(x));break;
            case 6:printf("%d\n",underGetNxt(x));break;
        }
    }
    return 0;
}
/*
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
*/

Splay

定义

俗称伸展树。也是一种二叉排序树，为了使整个查找时间变小，将被查频率高的那些节点转到靠近根节点的位置。每次查找节点之后对树进行重构，把被查找的节点搬移到树根。

为了将当前被访问节点旋转到树根，我们通常将节点自底向上旋转，直至该节点成为树根为止。“旋转”的巧妙之处就是在不打乱数列中数据大小关系（指中序遍历结果是全序的）情况下，所有基本操作的平摊复杂度仍为 $O(\log n)$。

一般来说， $Splay$ 的节点维护信息为：

$fa$ $chi[0/1]$ $dat$ $cnt$ $size$
父节点编号 子节点编号（一般 $0$ 为左子点，$1$ 为右子点） 节点权值 该节点权值出现的个数 子树大小

操作

旋转操作

与 $Treap$ 的旋转类似。

1
2
3
4
5
6
7
8
9
10
11
12
13
inline void underRotate(int x)
{
    int y=Tree[x].fa,z=Tree[y].fa;
    int k=Tree[y].chi[1]==x;
    Tree[z].chi[Tree[z].chi[1]==y]=x;
    Tree[x].fa=z;
    Tree[y].chi[k]=Tree[x].chi[k^1];
    Tree[Tree[x].chi[k^1]].fa=y;
    Tree[x].chi[k^1]=y;
    Tree[y].fa=x;
    underPushUp(y);
    underPushUp(x);
}

Splay操作

传递两个参数 $x$ 和 $k$ 表示将编号为 $x$ 的节点旋转到 $k$ 处，当 $k=0$ 时旋转到根节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline void Splay(int x,int k)
{
    while(Tree[x].fa!=k)
    {
        int y=Tree[x].fa,z=Tree[y].fa;
        if(z!=k)
            if((Tree[y].chi[1]==x)^(Tree[z].chi[1]==y))
                underRotate(x);
            else
                underRotate(y);
        underRotate(x);
    }
    if(!k) Root=x;
}

总的说其实就上面两句，但实际上还是要讨论很多情况的。背板子就完事儿了。

其他的就根据题目而定了。这里给出一些比较常用的操作：

插入操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
inline void underInsert(int x)
{
    int u=Root,p;
    while(u)
    {
        if(Tree[u].dat==x)
        {
            ++Tree[u].cnt;
            ++Tree[u].size;
            Splay(u,0);
            return ;
        }
        p=u;
        u=Tree[u].chi[x>Tree[u].dat];
    }
    u=++Idx;
    if(p) Tree[p].chi[x>Tree[p].dat]=u;
    Tree[u].dat=x;
    Tree[u].size=1;
    Tree[u].fa=p;
    Tree[u].cnt=1;
    Splay(u,0);
}

删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
inline void underErase(int x)
{
    int l=underGetPre(x),r=underGetNxt(x);
    Splay(l,0),Splay(r,l);
    Tree[Tree[r].chi[0]].cnt--;
    Tree[Tree[r].chi[0]].size--;
    if(!Tree[Tree[r].chi[0]].cnt)
    {
        Tree[Tree[r].chi[0]].fa=0;
        Tree[r].chi[0]=0;
    }
    Splay(r,0);
}

查找前驱操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
inline int underGetPre(int x)
{
    int u=Root,res,v=Root;
    while(u)
    {
        v=u;
        if(Tree[u].dat<x)
        {
            res=u;
            u=Tree[u].chi[1];
        }
        else u=Tree[u].chi[0];
    }
    Splay(v,0);
    return res;
}

查找后驱操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
inline int underGetNxt(int x)
{
    int u=Root,res,v=Root;
    while(u)
    {
        v=u;
        if(Tree[u].dat>x)
        {
            res=u;
            u=Tree[u].chi[0];
        }
        else u=Tree[u].chi[1];
    }
    Splay(v,0);
    return res;
}

查找排名操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
inline int underNum(int x)
{
    int u=Root;
    while(u)
    {
        if(Tree[Tree[u].chi[0]].size>=x) u=Tree[u].chi[0];
        else if(x<=Tree[Tree[u].chi[0]].size+Tree[u].cnt&&x>=Tree[Tree[u].chi[0]].size+1)
        {
            Splay(u,0);
            return u;
        }
        else
        {
            x-=Tree[Tree[u].chi[0]].size+Tree[u].cnt;
            u=Tree[u].chi[1];
        }
    }
}

AC Code

查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define underMax(x,y) ((x)>(y)?(x):(y))
#define underMin(x,y) ((x)<(y)?(x):(y))
typedef long long ll;
using namespace std;
const int MAXN=1e5+1;
const int INF=0x7f7f7f7f;
template<class T>
inline void underRead(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
int M,Idx;
struct Splay
{
    int chi[2],fa;
    int cnt,size,dat;
}Tree[MAXN];
int Root;
inline void underPushUp(int x)
{
    Tree[x].size=Tree[Tree[x].chi[0]].size+Tree[Tree[x].chi[1]].size+Tree[x].cnt;
}
inline void underRotate(int x)
{
    int y=Tree[x].fa,z=Tree[y].fa;
    int k=Tree[y].chi[1]==x;
    Tree[z].chi[Tree[z].chi[1]==y]=x;
    Tree[x].fa=z;
    Tree[y].chi[k]=Tree[x].chi[k^1];
    Tree[Tree[x].chi[k^1]].fa=y;
    Tree[x].chi[k^1]=y;
    Tree[y].fa=x;
    underPushUp(y);
    underPushUp(x);
}
inline void Splay(int x,int k)
{
    while(Tree[x].fa!=k)
    {
        int y=Tree[x].fa,z=Tree[y].fa;
        if(z!=k)
            if((Tree[y].chi[1]==x)^(Tree[z].chi[1]==y))
                underRotate(x);
            else
                underRotate(y);
        underRotate(x);
    }
    if(!k) Root=x;
}
inline void underInsert(int x)
{
    int u=Root,p;
    while(u)
    {
        if(Tree[u].dat==x)
        {
            ++Tree[u].cnt;
            ++Tree[u].size;
            Splay(u,0);
            return ;
        }
        p=u;
        u=Tree[u].chi[x>Tree[u].dat];
    }
    u=++Idx;
    if(p) Tree[p].chi[x>Tree[p].dat]=u;
    Tree[u].dat=x;
    Tree[u].size=1;
    Tree[u].fa=p;
    Tree[u].cnt=1;
    Splay(u,0);
}
inline void underInit()
{
    Root=++Idx;
    Tree[Root].fa=0;
    Tree[Root].cnt=1;
    Tree[Root].size=1;
    Tree[Root].dat=INF;
    underInsert(-INF);
}
inline int underGetPre(int x)
{
    int u=Root,res,v=Root;
    while(u)
    {
        v=u;
        if(Tree[u].dat<x)
        {
            res=u;
            u=Tree[u].chi[1];
        }
        else u=Tree[u].chi[0];
    }
    Splay(v,0);
    return res;
}
inline int underGetNxt(int x)
{
    int u=Root,res,v=Root;
    while(u)
    {
        v=u;
        if(Tree[u].dat>x)
        {
            res=u;
            u=Tree[u].chi[0];
        }
        else u=Tree[u].chi[1];
    }
    Splay(v,0);
    return res;
}
inline void underErase(int x)
{
    int l=underGetPre(x),r=underGetNxt(x);
    Splay(l,0),Splay(r,l);
    Tree[Tree[r].chi[0]].cnt--;
    Tree[Tree[r].chi[0]].size--;
    if(!Tree[Tree[r].chi[0]].cnt)
    {
        Tree[Tree[r].chi[0]].fa=0;
        Tree[r].chi[0]=0;
    }
    Splay(r,0);
}
inline int underNum(int x)
{
    int u=Root;
    while(u)
    {
        if(Tree[Tree[u].chi[0]].size>=x) u=Tree[u].chi[0];
        else if(x<=Tree[Tree[u].chi[0]].size+Tree[u].cnt&&x>=Tree[Tree[u].chi[0]].size+1)
        {
            Splay(u,0);
            return u;
        }
        else
        {
            x-=Tree[Tree[u].chi[0]].size+Tree[u].cnt;
            u=Tree[u].chi[1];
        }
    }
}
int main()
{
    // freopen("splay.in","r",stdin);
    // freopen("splay.out","w",stdout);
    underInit();
    underRead(M);
    for(int i=1;i<=M;++i)
    {
        int op,x;
        underRead(op),underRead(x);
        if(op==1) underInsert(x);
        else if(op==2) underErase(x);
        else if(op==3)
        {
            Splay(underGetPre(x),0);
            printf("%d\n",Tree[Tree[Root].chi[0]].size+Tree[Root].cnt);
        }
        else if(op==4) printf("%d\n",Tree[underNum(x+1)].dat);
        else if(op==5) printf("%d\n",Tree[underGetPre(x)].dat);
        else if(op==6) printf("%d\n",Tree[underGetNxt(x)].dat);
    }
    return 0;
}
/*
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
*/

文艺平衡树

例题

思路

我们已知，平衡树的中序遍历永远满足全序。我们又会发现（其实要推一下），当我们把区间 $[l,r]$ 反转时，就是将其两个子节点指针交换。将 $l$ 转到根节点，将 $r$ 转为 $l$ 的子节点。然后交换其子树编号即可。

AC Code

查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
#define underMax(x,y) ((x)>(y)?(x):(y))
#define underMin(x,y) ((x)<(y)?(x):(y))
typedef long long ll;
using namespace std;
const int MAXN=1e6+1;
const int INF=0x7f7f7f7f;
template<class T>
inline void underRead(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
int N,M,Idx;
struct Splay
{
    int chi[2],fa,tag;
    int cnt,size,dat;
}Tree[MAXN];
int Root;
inline void underPushUp(int x)
{
    Tree[x].size=Tree[Tree[x].chi[0]].size+Tree[Tree[x].chi[1]].size+1;
}
inline void underPushDown(int x)
{
	if(Tree[x].tag)
	{
		swap(Tree[x].chi[0],Tree[x].chi[1]);
		Tree[Tree[x].chi[0]].tag^=1;
		Tree[Tree[x].chi[1]].tag^=1;
		Tree[x].tag^=1;
	}
}
inline void underRotate(int x)
{
    int y=Tree[x].fa,z=Tree[y].fa;
    int k=Tree[y].chi[1]==x;
    Tree[z].chi[Tree[z].chi[1]==y]=x;
    Tree[x].fa=z;
    Tree[y].chi[k]=Tree[x].chi[k^1];
    Tree[Tree[x].chi[k^1]].fa=y;
    Tree[x].chi[k^1]=y;
    Tree[y].fa=x;
    underPushUp(y);
    underPushUp(x);
}
inline void Splay(int x,int k)
{
    while(Tree[x].fa!=k)
    {
        int y=Tree[x].fa,z=Tree[y].fa;
        if(z!=k)
            if((Tree[y].chi[1]==x)^(Tree[z].chi[1]==y)) underRotate(x);
            else underRotate(y);
        underRotate(x);
    }
    if(!k) Root=x;
}
inline void underInsert(int x)
{
    int u=Root,p=0;
    while(u)
    {
        if(Tree[u].dat==x)
        {
            ++Tree[u].cnt;
            ++Tree[u].size;
            Splay(u,0);
            return ;
        }
        p=u;
        u=Tree[u].chi[x>Tree[u].dat];
    }
    u=++Idx;
    if(p) Tree[p].chi[x>Tree[p].dat]=u;
    Tree[u].dat=x;
    Tree[u].size=1;
    Tree[u].fa=p;
    Tree[u].cnt=1;
    Splay(u,0);
}
inline void underWrite(int rt)
{
	underPushDown(rt);
	if(Tree[rt].chi[0]) underWrite(Tree[rt].chi[0]);
	if(Tree[rt].dat>1&&Tree[rt].dat<N+2) printf("%d ",Tree[rt].dat-1);
	if(Tree[rt].chi[1]) underWrite(Tree[rt].chi[1]);
}
inline int underKth(int k)
{
	int u=Root;
	while(1)
	{
		underPushDown(u);
		if(Tree[Tree[u].chi[0]].size>=k) u=Tree[u].chi[0];
		else if(Tree[Tree[u].chi[0]].size+1==k) return u;
		else k-=Tree[Tree[u].chi[0]].size+1,u=Tree[u].chi[1];
	}
}
inline void underSwap(int l,int r)
{
	l=underKth(l);
	r=underKth(r+2);
	Splay(l,0);
	Splay(r,l);
	Tree[Tree[Tree[Root].chi[1]].chi[0]].tag^=1;
}
inline void underInit()
{
    Root=++Idx;
    Tree[Root].fa=0;
    Tree[Root].cnt=1;
    Tree[Root].size=1;
    Tree[Root].dat=INF;
    underInsert(-INF);
}
int main()
{
    // freopen("splay.in","r",stdin);
    // freopen("splay.out","w",stdout);
    underRead(N),underRead(M);
    for(re int i=1;i<=N+2;++i) underInsert(i);
    for(re int i=1;i<=M;++i)
    {
    	int Ql,Qr;
        underRead(Ql),underRead(Qr);
        underSwap(Ql,Qr);
    }
    underWrite(Root);
    return 0;
}
/*
5 3
1 3
1 3
1 4
*/

Fhq-Treap

又称为无旋 $\text{Treap}$ ，顾名思义，不需要旋转的平衡树。

我们已经知道，$\text{Treap}$ 通过同时维护 $\text{Binary Search Tree}$ 和 $\text{Heap}$ 的性质以达到互相补充的平衡，而通过 $\text{priority}$ 的随机化属性，以及维护堆性质的操作，以达到一种随机的弱平衡，打乱结点的插入顺序，从而克服单调数据的退化链情况。

随机化下的期望复杂度可以保持在 $\mathcal O(\log_2 n)$ 左右，也使得有旋 $\text{Treap}$ 是普通平衡树中常数最小，也比较难卡的一种（相比 $\text{Splay}$）。

但是，并不是只有旋转一种方法能够同时维护树和堆的性质。还可以选择分裂与合并，从而 $\text{Fhq-Treap}$ ，也就是无旋 $\text{Treap}$ ，由此诞生。

介绍

实际上，$\text{Fhq-Treap}$ 和无旋 $\text{Treap}$ ，还不能等价。

无旋 $\text{Treap}$ 又称分裂合并 $\text{Treap}$ ，其核心操作在于分裂和合并。而不考虑各种旋转的平衡树，比大多数可旋平衡树好写得多。

也正是因为这样的操作方式，使得无旋 $\text{Treap}$ 支持维护序列，以及拥有可持久化的性质。

而 $\text{Fhq-Treap}$ （由范浩强提出的数据结构），就是可持久化且支持区间操作的无旋 $\text{Treap}$ 。

实现

按权分裂

写作 split(int cur,int key) 。

这两个参数分别代表根指针 $cur$ 和关键值 $key$ 。旨在将当前以 $cur$ 为根的 $\text{Treap}$ 分裂为两个 $\text{Treap}$ ，且第一个 $\text{Treap}$ 的所有结点的权值 $val$ 都小于等于 $key$ ，第二个 $\text{Treap}$ 的所有结点的权值都大于 $key$ 。

1
2
3
4
5
6
7
8
9
10
11
12
void split(int p,int k,int &u,int &v)
{
    if(!p) u=v=0;
    else
    {
        if(val[p]<=k)
            u=p,split(chi[p][1],k,chi[p][1],v);
        else
            v=p,split(chi[p][0],k,u,chi[p][0]);
        update(p);
    }
}

按排名分裂

写作 split(int cur,int rk) 。

表示当前 $\text{Treap}$ 的根指针 $cur$ 和排名 $rk$ 。

这样子的分裂会使原本的 $\text{Treap}$ 变为三个，其中第一个 $\text{Treap}$ 的结点排名小于 $rk$ ，第二个等于 $rk$ ，第三个大于。其中第二个 $\text{Treap}$ 有且仅有一个结点。

1
2
3
4
5
6
7
8
9
10
11
12
void split(int p,int k,int &u,int &v)
{
    if(!p) u=v=0;
    else
    {
        if(k<=siz[chi[p][0]])
            v=p,split(chi[p][0],k,u,chi[p][0]);
        else
            u=p,split(chi[p][1],k-siz[chi[p][0]]-1,chi[p][1],v);
        update(p);
    }
}

这里在网上找到一张分裂的示意图：

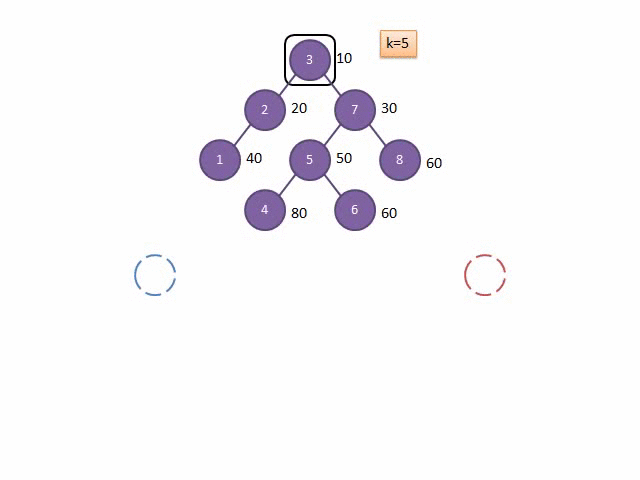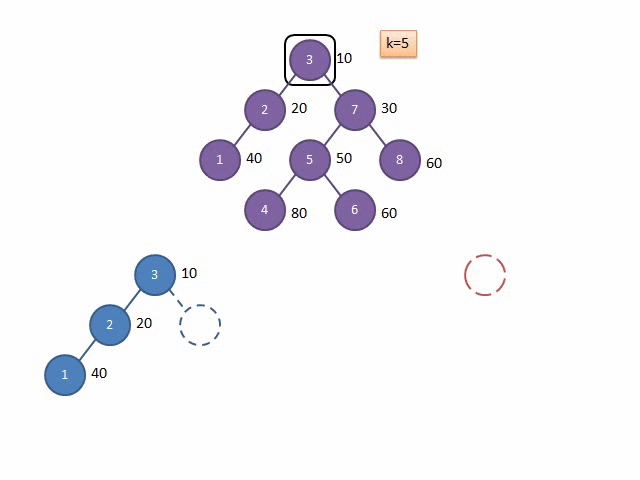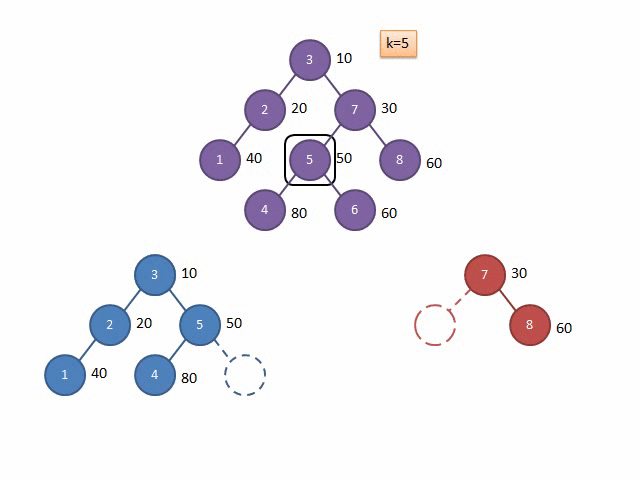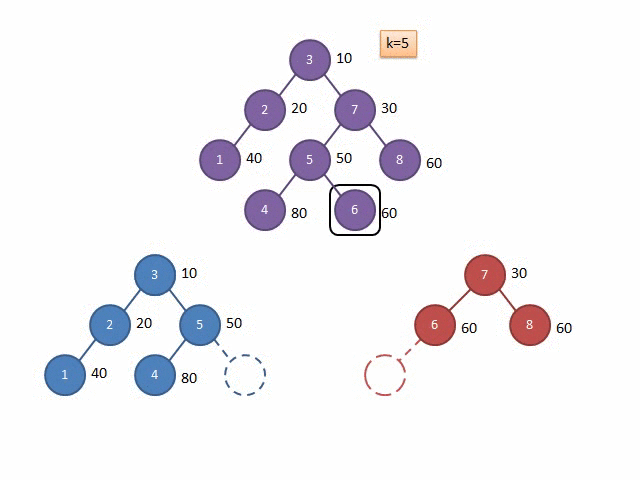
合并

写作 merge(int u,int v) 。

分别表示需要进行合并的两个 $\text{Treap}$ 的根指针。

此操作实现的条件是 $u$ 中所有结点权值都小于等于 $v$ 中所有结点的权值，即 $\max\{val_u\}\leq\min\{val_v\}$ 。不过，一般而言，所需要合并的两个 $\text{Treap}$ 都是从同一个 $\text{Treap}$ 分裂出去的，所以这个条件其实很好满足。

无旋 $\text{Treap}$ 首先是种 $\text{Treap}$ ，所以，我们需要使用合并操作来使其满足树和堆的性质。

由于第一个 $\text{Treap}$ 的权值较小，所以比较它的 $rd$ ，即附加权值。如果第一个树的 $rd$ 更小，则 $u$ 为新根，并将 $v$ 与 $u$ 的右子树合并；否则，将 $v$ 作为新根结点，并将 $u$ 与 $v$ 的左子树合并。

那么，明显地，合并操作需要使用递归实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int merge(int u,int v)
{
    if(!u||!v) return u+v;
    if(rd[u]<rd[v])
    {
        chi[u][1]=merge(chi[u][1],v);
        update(u);
        return u;
    }
    else
    {
        chi[v][0]=merge(u,chi[v][0]);
        update(v);
        return v;
	}
}

需要注意的是：$u$ 和 $v$ 调用的顺序会对答案产生影响。

其余操作

插入新数值

插入一个权值为 $v$ 的结点，则先把树按照 $v$ 的权值分裂，然后再按顺序合并。

1
2
3
4
5
inline void insert(int v)
{
    split(Rt,v,x,y);
    Rt=merge(merge(x,newNode(v)),y);
}

删除结点

删除权值为 $v$ 的点，则把树按照 $v$ 分裂为 $a,b$ ，并把 $a$ 按 $v-1$ 分裂为 $c,d$ ，先合并 $c$ 的两个儿子，然后执行 merge(merge(c,d),b) 。

1
2
3
4
5
6
inline void del(int v)
{
    split(Rt,v,x,z),split(x,v-1,x,y);
    y=merge(chi[y][0],chi[y][1]);
    Rt=merge(merge(x,y),z);
}

正确性证明？

先以 $v$ 分裂成 $a,b$ ，则现在 $v$ 在 $a$ 中，再将 $a$ 分裂为 $c,d$ 按 $v-1$ ，此时 $c$ 中的权值区间为 $[\min,v-1]$ ，而 $d$ 中就仅有 $v$ 一个结点，此时将 $d$ 的儿子合并，就是去除掉 $v$ 的影响，再把原来分裂的所有子树全部合并即可。

查询排名

对于权值为 $v$ 的排名，首先将整棵树以 $v-1$ 分裂，则 $x$ 树中的结点权值必定全部小于 $v$ ，则 $v$ 的排名就是 $siz[x]+1$ 。

1
2
3
4
5
6
7
inline int rank(int v)
{
    split(Rt,v-1,x,y);
    int res=siz[x]+1;
    Rt=merge(x,y);
    return res;
}

查询第 K

这个操作不必依赖分裂合并，就按照原树找就可以了。

1
2
3
4
5
6
7
8
9
inline int kth(int p,int k)
{
    while(1)
    {
        if(k<=siz[chi[p][0]]) p=chi[p][0];
        else if(k==siz[chi[p][0]]+1) return p;
        else k-=siz[chi[p][0]]+1,p=chi[p][1];
    }
}

查询前驱后继

对于查找 $v$ 的前驱，可以按 $v-1$ 划分，然后找到 $x$ 中最大的数；
对于查找 $v$ 的后继，可以按 $v$ 划分，然后找到 $y$ 中最小的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline int pre(int v)
{
    split(Rt,v-1,x,y);
    int res=val[kth(x,siz[x])];
    Rt=merge(x,y);
    return res;
}
inline int nxt(int v)
{
    split(Rt,v,x,y);
    int res=val[kth(y,1)];
    Rt=merge(x,y);
    return res;
}

区间操作

有一个模板，具体如何操作区间视题目而定。

将整棵树分裂成三棵，中间那一棵正好对应区间 $[l,r]$ ，然后就可以操作了。

1
2
3
4
5
6
7
inline void modify(int l,int r,int delta)	//这里的delta没有太大意义，只是代表操作
{
    int x,y,z;
    split(Rt,r,x,y),split(x,l-1,z,x);
    //modify(delta)
    merge(x,z,x),merge(Rt,x,y);
}

注意：涉及到区间操作的题时，只能够按照排名排序。

例题

普通平衡树

直接把上面的所有操作全部套上就好了。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline void write(T x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
const int MAXN=1e5+10;
int Q,opt,qx;
struct B_T
{
    int Idx=0,Rt=0,x,y,z;
    struct Treap
    {
        int siz,val,rd,chi[2];
    }Tree[MAXN];
    #define ls(p) Tree[p].chi[0]
    #define rs(p) Tree[p].chi[1]
    inline int newNode(int v)
    {
        Tree[++Idx]={1,v,rand()};
        return Idx;
    }
    inline void update(int p)
    {
        Tree[p].siz=Tree[ls(p)].siz+Tree[rs(p)].siz+1;
    }
    inline void split(int p,int k,int &u,int &v)
    {
        if(!p) u=v=0;
        else
        {
            if(Tree[p].val<=k) u=p,split(rs(p),k,rs(p),v);
            else v=p,split(ls(p),k,u,ls(p));
            update(p);
        }
        return ;
    }
    inline int merge(int u,int v)
    {
        if(!u||!v) return u+v;
        if(Tree[u].rd<Tree[v].rd)
        {
            rs(u)=merge(rs(u),v);
            update(u);
            return u;
        }
        else
        {
            ls(v)=merge(u,ls(v));
            update(v);
            return v;
        }
    }
    inline void insert(int v)
    {
        x=y=0;
        split(Rt,v,x,y);
        Rt=merge(merge(x,newNode(v)),y);
    }
    inline void del(int v)
    {
        x=y=z=0;
        split(Rt,v,x,z),split(x,v-1,x,y);
        y=merge(ls(y),rs(y));
        Rt=merge(merge(x,y),z);
    }
    inline int rank(int v)
    {
        x=y=0;
        split(Rt,v-1,x,y);
        int res=Tree[x].siz+1;
        Rt=merge(x,y);
        return res;
    }
    inline int kth(int p,int k)
    {
        while(1)
        {
            if(k<=Tree[ls(p)].siz) p=ls(p);
            else if(k==Tree[ls(p)].siz+1) return p;
            else k-=Tree[ls(p)].siz+1,p=rs(p);
        }
    }
    inline int pre(int v)
    {
        x=y=0;
        split(Rt,v-1,x,y);
        int res=Tree[kth(x,Tree[x].siz)].val;
        Rt=merge(x,y);
        return res;
    }
    inline int nxt(int v)
    {
        x=y=0;
        split(Rt,v,x,y);
        int res=Tree[kth(y,1)].val;
        Rt=merge(x,y);
        return res;
    }
}Tree;
int main()
{
    // freopen("fhq-treap.in","r",stdin);
    // freopen("fhq-treap.out","w",stdout);
    srand(time(NULL));
    read(Q);
    while(Q--)
    {
        read(opt,qx);
        if(opt==1) Tree.insert(qx);
        else if(opt==2) Tree.del(qx);
        else if(opt==3) write(Tree.rank(qx)),puts("");
        else if(opt==4) write(Tree.Tree[Tree.kth(Tree.Rt,qx)].val),puts("");
        else if(opt==5) write(Tree.pre(qx)),puts("");
        else if(opt==6) write(Tree.nxt(qx)),puts("");
    }
    return 0;
}
/*
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
*/

文艺平衡树

这个就会涉及到 $\text{FHQ-Treap}$ 的区间操作了。

没有想到用 $\text{FHQ-Treap}$ 写区间修改会比 $\text{Splay}$ 简单这么多。

对于翻转区间 $[l,r]$ ，就按照 $l-1$ 排名分离为 $x,y$ ，再把 $y$ 按照 $r-l+1$ 分离为 $y,z$ 从而提出区间，然后打上翻转标记即可。

前面已经提到过，翻转直接交换子结点指针即可并下传翻转标记。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline void write(T x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
const int MAXN=1e5+10;
int N,Q;
struct Fhq_Treap
{
    int Idx=0,Rt=0;
    int x,y,z;
    int siz[MAXN],val[MAXN],rd[MAXN],chi[MAXN][2];
    bool rev[MAXN];
    inline int newNode(int v)
    {
        siz[++Idx]=1,val[Idx]=v,rd[Idx]=rand();
        return Idx;
    }
    inline void update(int p)
    {
        siz[p]=siz[chi[p][0]]+siz[chi[p][1]]+1;
    }
    inline void reverse(int p)
    {
        if(!rev[p]) return ;
        std::swap(chi[p][0],chi[p][1]);
        if(chi[p][0]) rev[chi[p][0]]^=1;
        if(chi[p][1]) rev[chi[p][1]]^=1;
        rev[p]=0;
    }
    void split(int p,int k,int &u,int &v)
    {
        if(!p) u=v=0;
        else
        {
            if(rev[p]) reverse(p);
            if(siz[chi[p][0]]<k) u=p,split(chi[p][1],k-siz[chi[p][0]]-1,chi[p][1],v);
            else v=p,split(chi[p][0],k,u,chi[p][0]);
            update(p);
        }
    }
    int merge(int u,int v)
    {
        if(!u||!v) return u+v;
        if(rd[u]<rd[v])
        {
            if(rev[u]) reverse(u);
            chi[u][1]=merge(chi[u][1],v);
            update(u);
            return u;
        }
        else
        {
            if(rev[v]) reverse(v);
            chi[v][0]=merge(u,chi[v][0]);
            update(v);
            return v;
        }
    }
    inline void reverse(int l,int r)
    {
        x=y=z=0;
        split(Rt,l-1,x,y),split(y,r-l+1,y,z);
        rev[y]^=1;
        Rt=merge(x,merge(y,z));
    }
    void print(int p)
    {
        if(!p) return ;
        if(rev[p]) reverse(p);
        print(chi[p][0]);
        write(val[p]),putchar(' ');
        print(chi[p][1]);
    }
    inline void init(int n)
    {
        for(int i=1;i<=n;++i) Rt=merge(Rt,newNode(i));
    }
}Tree;
int main()
{
    // freopen("fhq-treap.in","r",stdin);
    // freopen("fhq-treap.out","w",stdout);
    srand(time(NULL));
    read(N,Q);
    Tree.init(N);
    for(int l,r;Q--;)
    {
        read(l,r);
        Tree.reverse(l,r);
    }
    Tree.print(Tree.Rt);
    return 0;
}
/*
5 3
1 3
1 3
1 4
*/

补充

一些注意事项：

  • 在很多平衡树（如 $\text{Treap,Splay}$ 等）里，对于同一权值的结点，会直接使用 $cnt$ 来统计；但无旋 $\text{Treap}$ 的每一个结点都是独立的，意味着对于同一权值而言，结点依然是不同的。
  • split() 和 merge() 的参数顺序对结果有非常大的影响，所以一定要把板子背牢。这里总结了一个没有正确性证明但好像确实是对的的结论：$u$ 在前，$v$ 在后。
  • 当查询 pre() 和 nxt() 时，需要判断当前子树是否存在，即当前数是否存在前驱后继，否则在查询 $k$ 时会进入死循环。可以选择建立卫兵（$inf,-inf$），但建立之后需要注意排名的变化；也可以选择特判。

没有更多了。

首次更新：$\text{date:2022.3.14}$

最后更新：$\text{date:2022.8.9}$

相关文章