Eternity

Until The End

自动机&最小表示法

发表于 更新于 分类于 ，
本文字数： 16k 阅读时长 ≈ 15 分钟

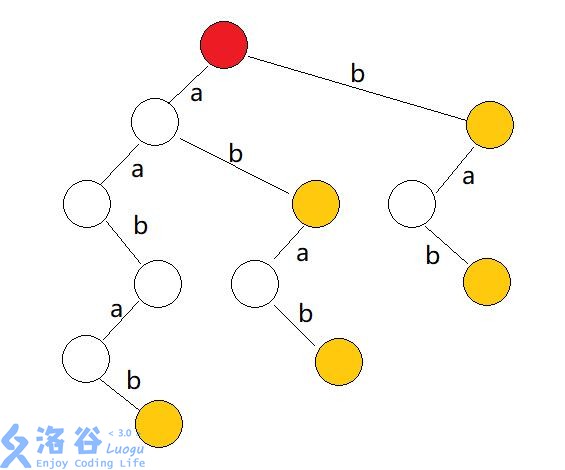
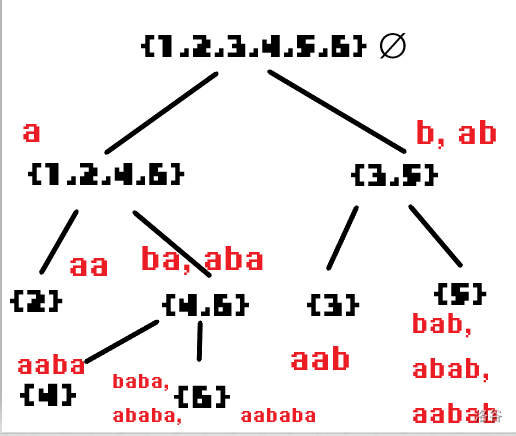
“能不能 $ \text{AC} $ 我不知道，自动倒是挺自动的。”

最小表示法

同构字符串

对于一个字符串 $S$ ，如果存在另一个字符串满足 $S_1\neq S$ ，但是将 $S$ 与 $S_1$ 无限循环之后的母串相同，则称 $S$ 与 $S_1$ 为同构字符串。如下：

$abca,bcaa,caab,aabc$ 则为该串的 $4$ 个循环同构字符串。

字符串的最小表示

对于一个字符串 $S[1\sim n]$ 与其所有的循环同构字符串中字典序最小的一个，称之为 $S$ 的最小表示。则对于上述循环同构字符串而言，其最小表示则为 $aabc$ 。

那么，怎么求最小表示呢？

很显然的一种思路是将这 $N$ 个字符串构造出来，然后逐一比较，这是最朴素的办法。时间复杂度会退化到 $\mathcal O(n^2)$ ，是极度不明智的做法。

我们可以使用指针扫描法，两两进行比对，当我们比较 $s[i]$ 和 $s[j]$ 时 ，直接向后扫描，依次取出 $k=0,1,2…,n$ 直到 $s[i+k]\neq s[j+k]$ ，然后进行比较。

那么，当 $s[i+k]\neq s[j+k]$ 时，如果 $s[i+k]>s[j+k]$ ，我们就可以知道 $s[i]$ 不会成为最小表示，因为 $s[j]>s[i]$ 是必然的。同理，我们也可以推出 $\forall 1\leq p\leq k,s[i+p]$ 都不会成为最小表示，因为这些字符串都包含了 $s[i+k]$ 并且满足 $s[i+k]>s[j+k]$ ，所以可以直接排除这些字符串的比较，也就可以直接执行 i=i+k+1; 一步。同样的，当 $s[i+k]<s[j+k]$ 时，执行 j=j+k+1; 即可。而 $ans=\min(i,j)$ 中的 $ans$ 即使最小表示字符串的头指针。

对于其复杂度，因为运行的限制条件在于 $i\leq n,j\leq n$ ，而 $i,j$ 必有其一在每一次运行中前进至少一步，则有 $i,j$ 总共移动次数不会超过 $2n$ ，那同理，时间复杂度就不会超过 $\mathcal O(n)$ ，我们就可以在线性时间内解决掉这个问题。

当然，为了不漏掉所有的字符串，我们需要在开始对字符串进行扩倍处理。

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
for(re int i=1;i<=N;++i) read(val[i]),val[i+N]=val[i];
while(i<=N&&j<=N)
{
    for(k=0;k<N&&val[i+k]==val[j+k];++k);
    if(k==N) break;
    if(val[i+k]>val[j+k])
    {
        i=i+k+1;
        if(i==j) ++i;
    }
    else
    {
        j=j+k+1;
        if(i==j) ++j;
    }
}
int ans=min(i,j);

对于 if(k==N) break; 的解释，是指当前字符串存在循环节，且 $i,j$ 恰好处于两个不同循环节的同一位置，导致之后的匹配全部成功。显然的，因为我们进行了扩倍，所以，当前字符串必定存在循环节且循环长度为 $n$ ，如果还尚不是很明白，读者可以自行纸上模拟，我想，最小表示法的纸上模拟应该还是比较简单的。

例题

Luogu P1368

将字符串转化为数组，其余不变。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
#define db double
typedef long long ll;
using namespace std;
const int MAXN=3e5+1;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
int N,val[MAXN<<2];
int main()
{
    // freopen("string.in","r",stdin);
    // freopen("string.out","w",stdout);
    read(N);
    for(re int i=1;i<=N;++i) read(val[i]),val[i+N]=val[i];
    int i=1,j=2,k;
    while(i<=N&&j<=N)
    {
        for(k=0;k<N&&val[i+k]==val[j+k];++k);
        if(k==N) break;
        if(val[i+k]>val[j+k])
        {
            i=i+k+1;
            if(i==j) ++i;
        }
        else
        {
            j=j+k+1;
            if(i==j) ++j;
        }
    }
    int ans=min(i,j);
    for(int l=ans;l<ans+N;++l) printf("%d ",val[l]);
    return 0;
}
/*

*/

自动机

前汁芝士：图论。

自动机，一般指“确定有限状态自动机”（称之为 DFA ）。OI Wiki上的解释大概是：

首先理解一下自动机是用来干什么的：自动机是一个对信号序列进行判定的数学模型。

这句话涉及到的名词比较多，逐一解释一下。“信号序列”是指一连串有顺序的信号，例如字符串从前到后的每一个字符、数组从 1 到 n 的每一个数、数从高到低的每一位等。“判定”是指针对某一个命题给出或真或假的回答。有时我们需要对一个信号序列进行判定。一个简单的例子就是判定一个二进制数是奇数还是偶数，较复杂的例子例如判定一个字符串是否回文，判定一个字符串是不是某个特定字符串的子序列等等。

自动机的工作原理和地图很类似。假设你在你家，然后你从你家到学校，按顺序经过了很多路口。每个路口都有岔路，而你在所有这些路口的选择就构成了一个序列。

例如，你的选择序列是“家门 -> 右拐 -> 萍水西街 -> 尚园街 -> 古墩路 -> 地铁站 -> 下宁桥”，那你按顺序经过的路口可能是“家 -> 家门口 -> 萍水西街竞舟北路口 -> 萍水西街尚圆街路口 -> 尚园街古墩路口 -> 古墩路中 -> 三坝地铁站 -> 下宁桥地铁站”。可以发现，上学的选择序列不止这一个。同样要去地铁站，你还可以从竞舟北路绕道，或者横穿文鼎苑抄近路。

而我们如果找到一个选择序列，就可以在地图上比划出这个选择序列能不能去学校。比如，如果一个选择序列是“家门 -> 右拐 -> 萍水西街 -> 尚园街 -> 古墩路 -> 地铁站 -> 钱江路 -> 四号线站台 -> 联庄”，那么它就不会带你去同一个学校，但是仍旧可能是一个可被接受的序列，因为目标地点可能不止一个。

也就是说，我们通过这个地图和一组目的地，将信号序列分成了三类，一类是无法识别的信号序列（例如“家门 -> ???”），一类是能去学校的信号序列，另一类是不能的信号序列。我们将所有合法的信号序列分成了两类，完成了一个判定问题。

既然自动机是一个数学模型，那么显然不可能是一张地图。对地图进行抽象之后，可以简化为一个有向图。因此，自动机的结构就是一张有向图。

而自动机的工作方式和流程图类似，不同的是：自动机的每一个结点都是一个判定结点；自动机的结点只是一个单纯的状态而非任务；自动机的边可以接受多种字符（不局限于 T 或 F）。

从起始结点开始，从高到低接受这个数的二进制序列，然后看最终停在哪里。如果最终停在红圈结点，则是偶数，否则不是。

如果需要判定一个有限的信号序列和另外一个信号序列的关系（例如另一个信号序列是不是某个信号序列的子序列），那么常用的方法是针对那个有限的信号序列构建一个自动机。这个在学习 KMP 的时候会讲到。

需要注意的是，自动机只是一个 数学模型，而 不是算法，也 不是数据结构。实现同一个自动机的方法有很多种，可能会有不一样的时空复杂度。

接下来你可以选择继续看自动机的形式化定义，也可以去学习 KMP、AC 自动机 或 SAM。

形式化定义

  1. 字符集 $\sum$ ，指该自动机能且仅能输入这些字符。
  2. 状态集合 $Q$ ，如果把 DFA 看做是一个有向图，那么 $Q$ 则是图上点的集合。
  3. 起始状态 $start$ ，满足 $start\in Q$ ，字面意思。
  4. 接受状态集合 $F$ ，满足 $F\subseteq Q$ ，似乎是一种特殊状态。
  5. 转移函数 $\delta$ ，可以看做是有向图的边，而边权是一个字母 $c$ ，走过这条边，则会在字符串后加上一个字符 $c$ 。

总而言之，自动机的学习并不在于自动机本身，而是以自动机为后缀名的一系列数据结构的学习。

AC自动机(AC-automaton)

说实话，我一直以为这是一个可以帮我自动 AC 的机器。天底下哪有比这还强的算法？？？

言归正传， AC 自动机是一种多模式串匹配算法。可以自行去了解一下自动机，反正我是没看太懂。用机房冬神的话来说，AC 自动机就是在 Trie 树上实现 KMP 。那么，前汁芝士当然就是 Trie 树和 KMP 啦。

那么步骤也就如出一辙了。

  1. 建树：将要读入的所有预处理字符串构造出一棵字典树(Trie-Tree)出来。
  2. 适配&失配：对字典树的所有节点构造其失配指针。
  3. 匹配：读入模式串，进行匹配。

步骤

建树

方法同字典树建树一样，将 n 个匹配串插入字典树即可。

1
2
3
4
5
6
7
8
9
10
void addString(char *s)
{
    int u=0,len=strlen(s+1);	//约定0为空根节点，字符串从1开始
    for(int i=1,c;i<=len;++i)
    {
        if(!ch[u][(c=s[i]-'a')]) ch[u][c]=++cnt;
        u=ch[u][c];
	}
    ++End[u];		//记录尾结点为u的字串的个数
}

失配

类似于 KMP 的配对方式，但又因为 Trie 树的模式串并不止一个，所以单独的匹配是不行的，而对于一个节点 $u$ ，其失配指针 $Fail[u]$ 可以满足的是其深度绝对比 $u$ 小。所以我们应该按照深度优先的顺序来进行失配，那也就自然而然地联想到 bfs 的使用了。使用 bfs 可以保证当我们配对 $u$ 的时候，其 $Fail[u]$ 点一定已经被配过了。

设 $u$ 到 $u$ 的儿子转移边上的字母是 $C$ ，则一直跳到节点 $v$ ，满足存在一条转移边是 $C$ ，那么就把 $u$ 的这个转移边的所指结点的失配指针指向 $v$ 的这条转移边所指的节点。如果直到根都没找到，则有 $Fail[u]=Root$ 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
inline void compare()
{
    queue<int>Q;
    for(int i=0;i<26;++i) if(ch[0][i]) Q.push(ch[0][i]);
    		//放入根节点
    while(!Q.empty())
    {
        int u=Q.front();Q.pop();
        for(int i=0;i<26;++i)		//遍历u的儿子
        {
            if(!ch[u][i]) ch[u][i]=ch[Fail[u]][i];
            						//没有该边，直接相连
            else
            {
                Q.push(ch[u][i]);
                Fail[ch[u][i]]=ch[Fail[u]][i];
                					//失配
            }
        }
    }
}

查询

依照 kmp 的方法查找母串中模式串的个数就行了。

这里是查询存在次数的代码：

1
2
3
4
5
6
7
8
9
10
11
12
inline void calc(char *s)
{
    int u=0,len=strlen(s+1);
    for(int i=1;i<=len;++i)
    {
        int c=s[i]-'a';
        u=ch[u][c];
        for(int j=u;j&&End[j]!=-1;j=Fail[j])
            ans+=End[j],End[j]=-1;		//避免重复
    }
    return ;
}

例题

Luogu P3808

如上所言。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
#define db double
typedef long long ll;
using namespace std;
const int MAXN=1e6+1;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
int N,ch[MAXN][30];
int ans,cnt,Fail[MAXN],son[MAXN];
char str[MAXN];
inline void addString(char *s)
{
    int u=0,len=strlen(s+1);
    for(int i=1;i<=len;++i)
    {
        int c=s[i]-'a';
        if(!ch[u][c]) ch[u][c]=++cnt;
        u=ch[u][c];
    }
    ++son[u];
    return ;
}
inline void compare()
{
    queue<int>Q;
    for(int i=0;i<26;++i) if(ch[0][i]) Q.push(ch[0][i]);
    while(!Q.empty())
    {
        int u=Q.front();Q.pop();
        for(int i=0;i<26;++i)
        {
            if(!ch[u][i]) ch[u][i]=ch[Fail[u]][i];
            else
            {
                Q.push(ch[u][i]);
                Fail[ch[u][i]]=ch[Fail[u]][i];
            }
        }
    }
}
inline void calc(char *s)
{
    int u=0,len=strlen(s+1);
    for(int i=1;i<=len;++i)
    {
        int c=s[i]-'a';
        u=ch[u][c];
        for(int j=u;j&&son[j]!=-1;j=Fail[j]) ans+=son[j],son[j]=-1;
    }
    return ;
}
int main()
{
    // freopen("AC-automaton.in","r",stdin);
    // freopen("AC-automaton.out","w",stdout);
    read(N);
    for(int i=1;i<=N;++i)
    {
        scanf("%s",str+1);
        addString(str);
    }
    compare();
    scanf("%s",str+1);
    calc(str);
    printf("%d",ans);
    return 0;
}
/*
4
a
ab
ac
abc
abcd
*/

Luogu P3796 加强版

从统计所有，到分开统计，我们可以多使用一个数组 $Idx[x]$ 表示以节点 $x$ 结束的模式串的编号是多少。然后在查询的时候，然后在 $T[i]$ 中统计每一个编号所匹配的所有子串的个数，最后当该点的 $Idx[u]$ 有确值，统计进 $Cnt[Idx[u]]$ 即可。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
#define db double
typedef long long ll;
using namespace std;
const int MAXN=151;
const int MAXS=71;
const int MAXT=1e6+1;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
int N,Test;
char str[MAXN][MAXS],Tr[MAXT];
int Tre[MAXT][27],Cnt,Idx[MAXT],Sum[MAXN],Tot[MAXT];
int Fail[MAXT],ans;
inline void init()
{
    memset(Idx,0,sizeof(Idx));
    memset(Sum,0,sizeof(Sum));
    memset(Tre,0,sizeof(Tre));
    memset(Tot,0,sizeof(Tot));
    memset(Fail,0,sizeof(Fail));
    Cnt=0;
}
inline void addString(char *s,int id)
{
    int u=0,len=strlen(s+1);
    for(int i=1;i<=len;++i)
    {
        if(!Tre[u][s[i]-'a']) Tre[u][s[i]-'a']=++Cnt;
        u=Tre[u][s[i]-'a'];
    }
    Idx[u]=id;
    return ;
}
inline void pareString()
{
    queue<int>Q;
    for(int i=0;i<26;++i) if(Tre[0][i]) Q.push(Tre[0][i]);
    while(!Q.empty())
    {
        int u=Q.front();Q.pop();
        for(int i=0;i<26;++i)
        {
            if(!Tre[u][i]) Tre[u][i]=Tre[Fail[u]][i];
            else
            {
                Q.push(Tre[u][i]);
                Fail[Tre[u][i]]=Tre[Fail[u]][i];
            }
        }
    }
}
inline int query(char *s)
{
    int u=0,len=strlen(s+1),res=0;
    for(int i=1;i<=len;++i)
    {
        u=Tre[u][s[i]-'a'];
        for(int j=u;j;j=Fail[j]) ++Tot[j];
    }
    for(int i=0;i<=Cnt;++i)
        if(Idx[i]) checkMax(res,Tot[i]),Sum[Idx[i]]=Tot[i];
    return res;
}
int main()
{
    // freopen("AC-automaton.in","r",stdin);
    // freopen("AC-automaton.out","w",stdout);
    read(N);
    while(N)
    {
        init();
        for(int i=1;i<=N;++i)
        {
            scanf("%s",str[i]+1);
            addString(str[i],i);
        }
        pareString();
        scanf("%s",Tr+1);
        printf("%d\n",ans=query(Tr));
        for(int i=1;i<=N;++i)
            if(Sum[i]==ans) printf("%s\n",str[i]+1);
        read(N);
    }
    return 0;
}
/*
2
aba
bab
ababababac
6
beta
alpha
haha
delta
dede
tata
dedeltalphahahahototatalpha
0
*/

后缀自动机SAM(Suffix Automaton)

概念

对于一个字符串 $s$ 的 SAM 而言，是一个接受 $s$ 的所有后缀子串（包括 $s$ 本身）的最小 DFA 。首先给出个例子：

SAM

对于该字符串 $s=’aabab’$ 而言，其后缀子串包括 $’aabab’,’abab’,’bab’,’ab’,’b’$ 即可。这就是一个最朴素的后缀自动机的字典树，但是，我们会发现会存在非常多相等的子树存在，会浪费非常多不必要的空间，最多会达到 $\mathcal O(n^2)$ ，这是不允许的。

那么，有没有办法将空间优化到 $\mathcal O(n)$ ，线性？很困难？所以才会有仙人创造出后缀自动机。

线性时间下的后缀自动机

后缀自动机的性质：

  1. SAM 是一个 DAG （有向无环图）。结点被称作状态，边被称作状态间的转移。
  2. 图存在源点 $t_0$ ，被称作初始状态，其余所有结点都可从 $t_0$ 出发到达。
  3. 存在一个或多个终止状态。从 $t_0$ 出发，最终转移到一个终止状态，路径所连接的一个字符串必定为 $s$ 的后缀；反之， $s$ 的任意后缀均可用一条从 $t_0$ 到某个终止状态的路径表示。
  4. SAM 是满足上述条件的所有自动机中，结点数最少的。

Endpos

记一个数组的每一个元素都是集合，记作 $Endpos[i]$ ，以 $s=’aabab’$ 为例，则有 $Endpos[‘ab’]=\{3,5\}$ 。那么显然，有以下性质：

  1. 设字符串 $s$ 中的两个非空子串 $u$ 和 $v$ ，假定 $|u|\leq |v|$ ，且满足 $Endpos(u)=Endpos(v)$ ，那么 $u$ 的每一次出现，都是以 $w$ 的后缀的形式出现的。
  2. 同样，满足：$\begin{split} \left \{ \begin{array}{ll} Endpos(u)\subseteq Endpos(v) & \text{if}\ u\ \text{is a suffix of }w\\ Endpos(u)\cap Endpos(v)=\varnothing & otherwise \end{array} \right. \end{split}$
  3. 对于一个 $Endpos$ 的等价类，将类中的所有子串按长度非递增的顺序排序。每个子串都不会比它前一个子串长，与此同时每个子串也是它前一个子串的后缀。换句话说，对于同一等价类的任一两子串，较短者为较长者的后缀，且该等价类中的子串长度恰好覆盖整个区间 $[x,y]$ 。
  4. 等价类没有相同长度的字符串。

对于一个非 $t_0$ 的状态 $v$ ，必然对应于具有相同 $Endpos$ 的等价类。定义 $w$ 是这些字符串中最长的一个，则其他字符串必定是 $w$ 的后缀。

而对于 $w$ 的最长的几个后缀全部包含于这个等价类，且所有其他后缀（包括空后缀），在其他等价类中。记 $t$ 为满足上述要求最长的后缀，将 $v$ 的后缀链接 $Link[v]$ 与 $t$ 连接。那么，

一个后缀链接 $Link[v]$ 连接到对应于 $w$ 的最长后缀的另一个 $Endpos$ 等价类的状态。

则有

  1. 所有后缀链接构成了一棵以 $t_0$ 为根节点的树。
  2. 通过 $Endpos$ 集合构造的树（子节点集合包含于父节点集合，类似于线段树）与通过后缀链接 $Link$ 构造的树相同。

Parent Tree

以父子关系构建的树（类似于高中男寝的现状）。有这么一张图：

PT

是对应 $s=’aababa’$ 的 Parent Tree 。显而易见地，可以看见很多性质，类似于：

  • 子节点是父节点的子集，且其表示的后缀串大小依次递增且父节点表示的字符串都是子节点的后缀子串。

而后缀自动机的构造所需要的状态，正是父母树中的所有状态（可以认为同一个字符串的 SAM 和 Parent Tree 共用同样的节点），但边有所不同。但 Parent Tree 的根就是 PAM 中的 $t_0$ ，即源点。而终止节点就是包含了原串的节点，如上图的 $6$ 号节点。那么，我们的任务，就是在此原点中，构建出一个有向无环图，使其路径，有且仅有原字符串 $s$ 的所有后缀子串。

构造

首先，后缀自动机的构造算法是一个在线算法， 我们逐一读入字符串中的每一个字符，并对应维护后缀自动机。为了保证线性的空间复杂度，每一个状态仅有两个元素表示为 $len$ 和 $link$ 。

首先，初始化整个后缀自动机，创立空根节点满足 $len[t_0]=0,link[t_0]=-1,last=0,cnt=0$ ，$-1$ 表示虚空根，初始长度为 $0$ ，$cnt$ 是当前节点编号与总结点数。$last$ 表示在添加字符 $c$ 时，整个自动机对应的状态。

接着，

读入字符 $c$ ，为字符 $c$ 创建一个新的状态记为 $cur$ ，并使 $len[cur]=len[last]+1$ 。

从状态 $last$ 开始，遍历后缀链接数组 $link[]$ ，寻找是否存在某个点已经有了到 $c$ 的转移，并将该点记为 $p$ 。

如果不存在，则 $p=-1$ ，且 $c$ 字符是第一次在该字符串中出现。则运行 $link[cur]=0$ 并退出。

如果存在状态 $p\neq -1$ 则令 $p$ 通过 $c$ 转移到的状态为 $q$ 。如果有 $len[p]+1=len[q]$ 的话，则有 $link[cur]=q$ ；否则，

对于状态 $cur$ 与当前节点 $p’$ 所指的 $q$ 而言，他们必定有一段公共后缀（至少包含一个字符 $c$ ）。然后，我们创建一个新状态记为 $clone$ ，并满足 $len[clone]=len[p]+1$ ，并让 $q$ 和 $cur$ 都指向 $clone$ ，即让 $clone$ 成为 $q$ 和 $cur$ 的父节点。让 $clone$ 代替 $q$ 的存在，使所有曾转移至 $q$ 的边全部定向指向 $clone$ 即可。

最后，将 $last$ 更新为 $cur$ 即可。我们从 $last$ 开始，遍历后缀链接直到 $t_0$ ，将所有经过的状态记为终止节点，那么，从 $t_0$ 到任意终止节点的路径所构成的字符串，包含且仅包含所有 $s $ 的后缀子串。这些被标记的状态，也全部都是终止状态。

对于上述所有的证明与拓展讲解，详见OI Wiki

例题

Luogu P3804

构造不用多说，运用在于查找一个子串出现的个数。最后的统计可以使用拓扑排序或者深度优先搜索。我的拓扑似乎炸了，换了 dfs 才过的。计算出现次数，只需要将 $EndposSize[Link[u]]+=EndposSize[u]$ 即可。

AC Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
#define db double
typedef long long ll;
using namespace std;
const int MAXN=2e6+1;
template<class T>
inline void read(T &x)
{
    x=0;
    char ch=gh(),t=0;
    while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
    if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
    read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
    return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
    return x>y?x=y,1:0;
}
char Str[MAXN];
namespace SAM
{
    struct State
    {
        int len,link,next[27];
    }Tre[MAXN<<1];
    struct Path
    {
        int next,to;
    }Edge[MAXN<<1];
    int Total,Head[MAXN];
    inline void addEdge(int u,int v)
    {
        Edge[++Total]=(Path){Head[u],v};Head[u]=Total;
    }
    int Last,Size=0,Endpos[MAXN],T[MAXN],A[MAXN];
    ll ans=0;
    inline void init()
    {
        Tre[1].len=0,Tre[1].link=0;
        Last=1,Size=1;
        memset(Endpos,0,sizeof(Endpos));
        memset(T,0,sizeof(T));
        memset(A,0,sizeof(A));
    }
    inline void Extend(char c)
    {
        int cur=++Size;
        Tre[cur].len=Tre[Last].len+1;
        int p=Last;
        Endpos[cur]=1;
        while(p&&!Tre[p].next[c-'a'])
        {
            Tre[p].next[c-'a']=cur;
            p=Tre[p].link;
        }
        if(!p) Tre[cur].link=1;
        else
        {
            int q=Tre[p].next[c-'a'];
            if(Tre[p].len+1==Tre[q].len) Tre[cur].link=q;
            else
            {
                int clone=++Size;
                Tre[clone]=Tre[q];
                Tre[clone].len=Tre[p].len+1;
                while(p&&Tre[p].next[c-'a']==q)
                {
                    Tre[p].next[c-'a']=clone;
                    p=Tre[p].link;
                }
                Tre[q].link=Tre[cur].link=clone;
            }
        }
        Last=cur;
    }
    void dfs(int x)
    {
        for(int e=Head[x];e;e=Edge[e].next)
        {
            dfs(Edge[e].to);
            Endpos[x]+=Endpos[Edge[e].to];
        }
        ll res=Endpos[x]*Tre[x].len;
        if(Endpos[x]!=1) checkMax(ans,res);
    }
    inline void calc()
    {
        for(int i=2;i<=Size;++i) addEdge(Tre[i].link,i);
        dfs(1);
        printf("%lld",ans);
    }
};
using namespace SAM;
int main()
{
    // freopen("suffix-automaton.in","r",stdin);
    // freopen("suffix-automaton.out","w",stdout);
    scanf("%s",Str+1);
    int Len=strlen(Str+1);
    SAM::init();
    for(int i=1;i<=Len;++i) SAM::Extend(Str[i]);
    SAM::calc();
    return 0;
}
/*
abab
*/

后话

可以证明，最终 Parent Tree 和 SAM 所依赖的那个图 $G(V,E)$ ，满足 $V\leq n,E\leq n$ ，即这张图的边数和点数都是 $\mathcal O(n)$ 的。证明较复杂，读者可以自行搜索阅读。

相关文章